
Solved Use Part 1 Of The Fundamental Theorem Of Calculus To Chegg There are 3 steps to solve this one. use part i of the fundamental theorem of calculus to find each derivative, given the following f (x) : f (x)=∫ 3x 1 t31 dt f ′(x)= f ′(1)= use part i of the fundamental theorem of calculus to find the derivative of f (x)=∫ −5x t3 53dt f ′(x)= [note: enter a function as your answer. The fundamental theorem of calculus, part 1 shows the relationship between the derivative and the integral. the fundamental theorem of calculus, part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. the total area under a curve can be found using this formula.
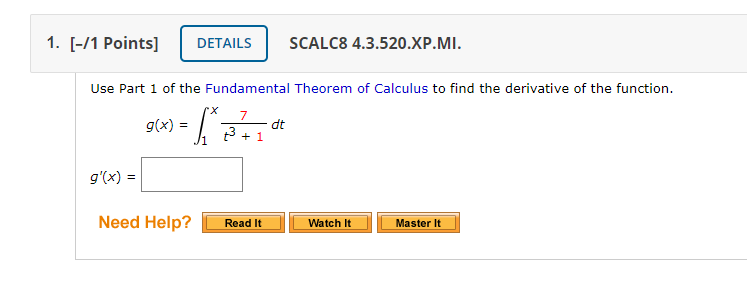
Solved Use Part 1 Of The Fundamental Theorem Of Calculus Chegg You have to use chain rule (of derivatives) combined with fundamental theorem of calculus part 1. put $u=\sqrt{x} $ and then we have $$\frac{d} {dx} \int {\sqrt{x}} ^{\pi 4}\theta\tan\theta\, d\theta=\left(\frac {d} {du} \int {u} ^{\pi 4}\theta \tan\theta\, d\theta\right)\frac{du} {dx} =( u\tan u)\frac{1}{2\sqrt{x}}= \frac{1}{2}\tan\sqrt{x} $$. This video gives five examples of how to take the derivative of an integral using the fundamental theorem of calculus (ftc) part i. some examples involve using integral properties to get. Use part i of the fundamental theorem of calculus to find the derivative of: h (x) = ∫ (top of the integral symbol says "sin (x)" and bottom of integral symbol says " 3") then followed by the equation (cos (t^5) t)dt. h' (x) = ?? so: let's talk about what the derivative would be if, instead of "sin (x)", the upper limit of integration were "x". Use part i of the fundamental theorem of calculus to find each derivative, given the following f(x): po 1 f(x) = ? 5 dt 13 it t2 at f'(x) = preview f'(14) = preview.

Solved Use Part I Of The Fundamental Theorem Of Calculus To Chegg Use part i of the fundamental theorem of calculus to find the derivative of: h (x) = ∫ (top of the integral symbol says "sin (x)" and bottom of integral symbol says " 3") then followed by the equation (cos (t^5) t)dt. h' (x) = ?? so: let's talk about what the derivative would be if, instead of "sin (x)", the upper limit of integration were "x". Use part i of the fundamental theorem of calculus to find each derivative, given the following f(x): po 1 f(x) = ? 5 dt 13 it t2 at f'(x) = preview f'(14) = preview. Use the fundamental theorem of calculus, part 1, to evaluate derivatives of integrals. state the meaning of the fundamental theorem of calculus, part 2. use the fundamental theorem of calculus, part 2, to evaluate definite integrals. explain the relationship between differentiation and integration. Use part 1 of the fundamental theorem of calculus to find the derivative of the function. g (x) = 3x u2 − 5 u2 5 du 2x hint: 3x f (u) du 2x = 0 f (u) du 2x 3x f (u) du 0. the fundamental theorem of calculus part 1 states that if a function f is continuous over the interval [a, b] and f is an antiderivative of f on [a, b], then:. (a)find f0(x) by using part(i)of the fundamental theorem of calculus. (b)find f0(x) by rst using part(ii)of the fundamental theorem of calculus to evaluate the integral. solution (a)part(i)gives f0(x) = d dx z x 1 (4t 3)dt = 4x 3:. Fundamental theorem of calculus (part 1) example: find g0(x) if g(x) = z x2 3 et2 dt. solution: let h(u) = z u 3 et2 dt. then h 0(u) = eu2. however, g(x) = h(x2) so the chain rule tells us that g0(x) = h 0(x2) . d dx copyrighted x2 = e(x2)2 (2x) = 2xex4.

Solved 5 Use The Fundamental Theorem Of Calculus Part 1 To Chegg Use the fundamental theorem of calculus, part 1, to evaluate derivatives of integrals. state the meaning of the fundamental theorem of calculus, part 2. use the fundamental theorem of calculus, part 2, to evaluate definite integrals. explain the relationship between differentiation and integration. Use part 1 of the fundamental theorem of calculus to find the derivative of the function. g (x) = 3x u2 − 5 u2 5 du 2x hint: 3x f (u) du 2x = 0 f (u) du 2x 3x f (u) du 0. the fundamental theorem of calculus part 1 states that if a function f is continuous over the interval [a, b] and f is an antiderivative of f on [a, b], then:. (a)find f0(x) by using part(i)of the fundamental theorem of calculus. (b)find f0(x) by rst using part(ii)of the fundamental theorem of calculus to evaluate the integral. solution (a)part(i)gives f0(x) = d dx z x 1 (4t 3)dt = 4x 3:. Fundamental theorem of calculus (part 1) example: find g0(x) if g(x) = z x2 3 et2 dt. solution: let h(u) = z u 3 et2 dt. then h 0(u) = eu2. however, g(x) = h(x2) so the chain rule tells us that g0(x) = h 0(x2) . d dx copyrighted x2 = e(x2)2 (2x) = 2xex4.

Solved Use Part Ii Of The Fundamental Theorem Of Calculus Chegg (a)find f0(x) by using part(i)of the fundamental theorem of calculus. (b)find f0(x) by rst using part(ii)of the fundamental theorem of calculus to evaluate the integral. solution (a)part(i)gives f0(x) = d dx z x 1 (4t 3)dt = 4x 3:. Fundamental theorem of calculus (part 1) example: find g0(x) if g(x) = z x2 3 et2 dt. solution: let h(u) = z u 3 et2 dt. then h 0(u) = eu2. however, g(x) = h(x2) so the chain rule tells us that g0(x) = h 0(x2) . d dx copyrighted x2 = e(x2)2 (2x) = 2xex4.
