
Solved Use Part Ii Of The Fundamental Theorem Of Calculus Chegg Use part ii of the fundamental theorem of calculus to find the derivative of the following functions: g(x) = x integrate 1 (2 t^4)^5 dt y(x) = 0 integrate x^1 2 sin^3(t)dt f(x) = 4 integrate x cos (t^5) dt g(x) = x^2 integrate squareroot x squareroot t sin(t) dt h(x) = x^2 integrate 0 3 squareroot 1 r^3 dr a population of rabbits at time t. Fundamental theorem of calculus is the basic theorem that is widely used for defining a relation between integrating a function of differentiating a function. the fundamental theorem of calculus is widely useful for solving various differential and integral problems and making the solution easy for students.
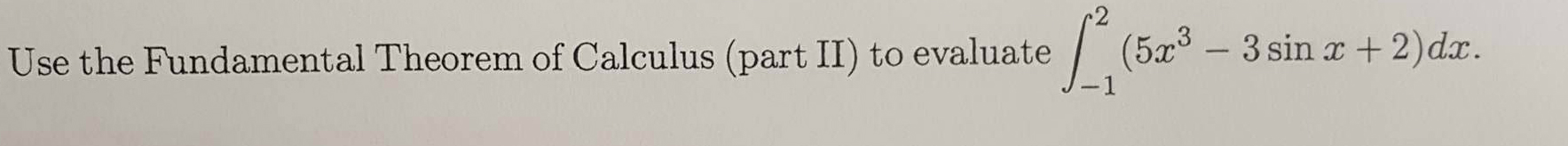
Solved Use The Fundamental Theorem Of Calculus Part Ii To Chegg Using the fundamental theorem of calculus, we have f′(x) = x2 sin x f ′ (x) = x 2 sin x. this simple example reveals something incredible: f(x) f (x) is an antiderivative of x2 sin x x 2 sin x! therefore, f(x) = 13x3 − cos x c f (x) = 1 3 x 3 − cos x c for some value of c c. (we can find c c, but generally we do not care. Use part 2 of the fundamental theorem of calculus to decide if the definite integral exists and either evaluate the integral or enter dne if it does not exist. there are 2 steps to solve this one. the fundamental theorem of calculus, part 2, states that if (f) is continuous on (a b) and (f) is an antideriva not the question you’re looking for?. (a)find f0(x) by using part(i)of the fundamental theorem of calculus. (b)find f0(x) by rst using part(ii)of the fundamental theorem of calculus to evaluate the integral. solution (a)part(i)gives f0(x) = d dx z x 1 (4t 3)dt = 4x 3:. Note that the rst part of the fundamental theorem of calculus only allows for the derivative with respect to the upper limit (assuming the lower is constant). in this case, however, the upper limit isn’t just x, but rather x4. we want, as earlier, to nd d dx z x4 0 cos2( ) d but the fundamental theorem applies to d dx4 z x4 0 cos2( ) d the.

Solved Exercise 5 The Fundamental Theorem Of Calculus Part Chegg (a)find f0(x) by using part(i)of the fundamental theorem of calculus. (b)find f0(x) by rst using part(ii)of the fundamental theorem of calculus to evaluate the integral. solution (a)part(i)gives f0(x) = d dx z x 1 (4t 3)dt = 4x 3:. Note that the rst part of the fundamental theorem of calculus only allows for the derivative with respect to the upper limit (assuming the lower is constant). in this case, however, the upper limit isn’t just x, but rather x4. we want, as earlier, to nd d dx z x4 0 cos2( ) d but the fundamental theorem applies to d dx4 z x4 0 cos2( ) d the. Answer the fundamental theorem of calculus, part 2, states that if a function f is continuous over the interval [a, b] and f is an antiderivative of f on [a, b], then: ∫[a, b] f(t). That's why in the fundamental theorem of calculus part 2, the choice of the antiderivative is irrelevant since every choice will lead to the same final result. on the other hand, $g(x)=\int a^x f(t)\; dt$ is a special antiderivative of $f$: it is the antiderivative of $f$ whose value at $a$ is $0$. so $g(a)=0$ by definition of $g$. Overview: we discussed part i of the fundamental theorem of calculus in the last section. we establish part ii of the theorem here. we also show how part ii can be used to prove part i and how it can be combined with the chain rule to find derivatives of integrals with functions as limits of integration. Use part 2 of the fundamental theorem of calculus to decide if the definite integral exists and either evaluate the integral or enter dne if it does not exist. ∫ 0 1 (4 x x ) d x.
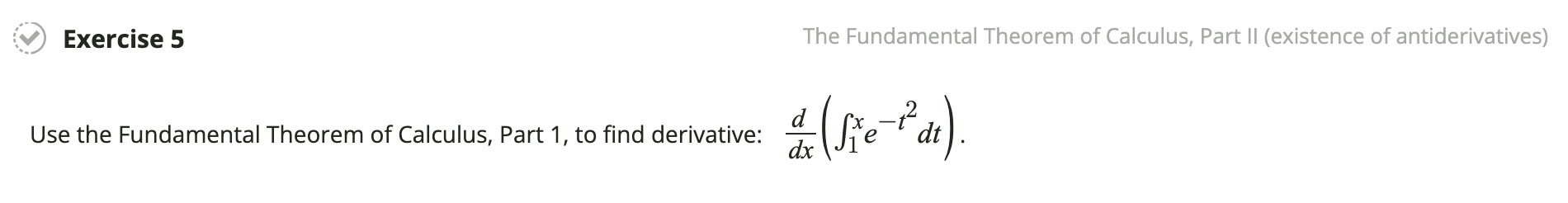
Solved Exercise 5 The Fundamental Theorem Of Calculus Part Chegg Answer the fundamental theorem of calculus, part 2, states that if a function f is continuous over the interval [a, b] and f is an antiderivative of f on [a, b], then: ∫[a, b] f(t). That's why in the fundamental theorem of calculus part 2, the choice of the antiderivative is irrelevant since every choice will lead to the same final result. on the other hand, $g(x)=\int a^x f(t)\; dt$ is a special antiderivative of $f$: it is the antiderivative of $f$ whose value at $a$ is $0$. so $g(a)=0$ by definition of $g$. Overview: we discussed part i of the fundamental theorem of calculus in the last section. we establish part ii of the theorem here. we also show how part ii can be used to prove part i and how it can be combined with the chain rule to find derivatives of integrals with functions as limits of integration. Use part 2 of the fundamental theorem of calculus to decide if the definite integral exists and either evaluate the integral or enter dne if it does not exist. ∫ 0 1 (4 x x ) d x.

Solved Exercise 5 The Fundamental Theorem Of Calculus Part Chegg Overview: we discussed part i of the fundamental theorem of calculus in the last section. we establish part ii of the theorem here. we also show how part ii can be used to prove part i and how it can be combined with the chain rule to find derivatives of integrals with functions as limits of integration. Use part 2 of the fundamental theorem of calculus to decide if the definite integral exists and either evaluate the integral or enter dne if it does not exist. ∫ 0 1 (4 x x ) d x.

Solved Second Fundamental Theorem Of Calculus 3 Use The 2nd Chegg
