Solved Use Rational Roots Theorem And Find All Rational Chegg

By forhairstyles On Aug 25, 2025

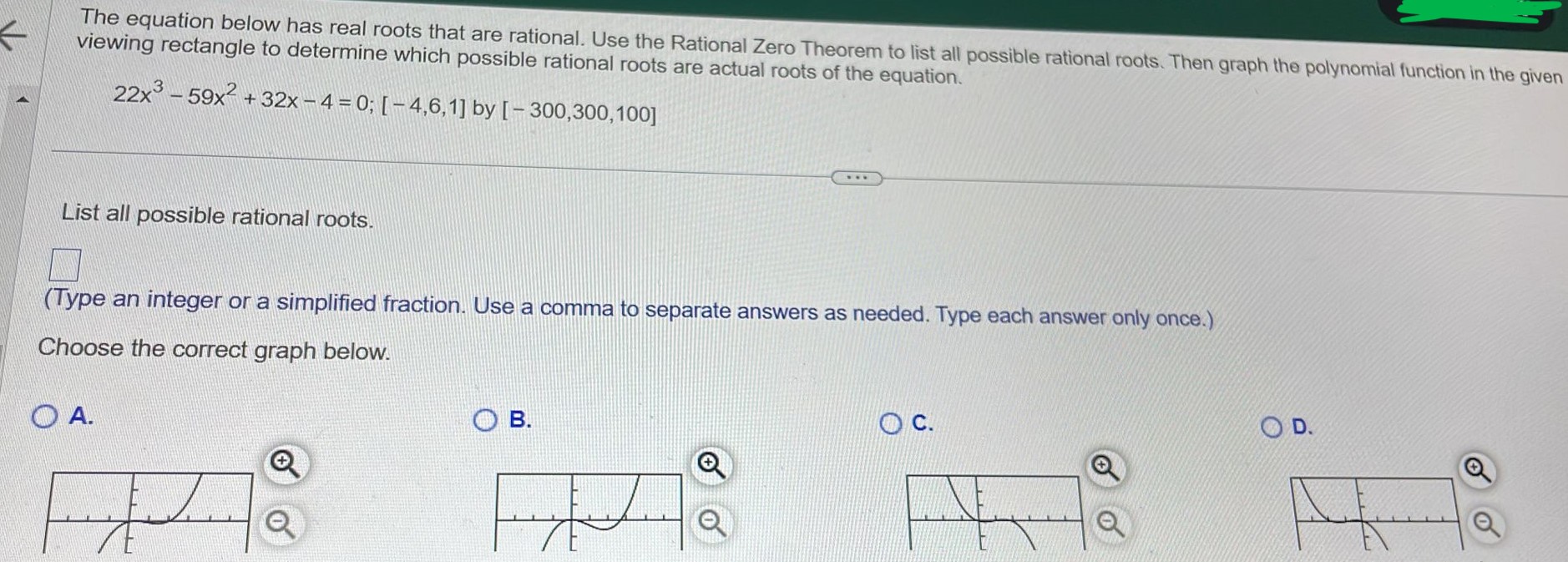
Solved The Equation Below Has Real Roots That Are Rational Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: use rational roots theorem and find all rational roots of the following equation 80x3 42x2−35x 3=0 show transcribed image text. Quicker way to find factors using the rational root theorem? i get how to do the steps of it and use synthetic division to find the factor that works, but it's really long and time consuming. is there any way to narrow down the options quicker?.

Solved Use Rational Roots Theorem And Find All Rational Chegg Free rational roots calculator find roots of polynomials using the rational roots theorem step by step. State the possible rational zeros for each function. then find all rational zeros. rational zeros: , 5, −1 mult. no. that would be like factoring 740 and discovering 3 isn't a factor but then checking if anything 740 breaks down into has a factor of 3. Use the rational root theorem to list all possible rational roos for the equation. determine what descartes' rule of signs says about the number of positive and negative real roots for the polynomial function. a polynomial function p (x) with rational coefficients has the given roots. find two additional roots of p (x)=0. Using rational roots theorem and synthetic division, find all the real zeros of the polynomial function. f (x) = x^3 4x^2 4x 16. the rational roots theorem states that if a polynomial has a rational root, p q, then p is a factor of the constant term and q is a factor of the leading coefficient.

Solved Use Rational Roots Theorem And Find All Rational Chegg Use the rational root theorem to list all possible rational roos for the equation. determine what descartes' rule of signs says about the number of positive and negative real roots for the polynomial function. a polynomial function p (x) with rational coefficients has the given roots. find two additional roots of p (x)=0. Using rational roots theorem and synthetic division, find all the real zeros of the polynomial function. f (x) = x^3 4x^2 4x 16. the rational roots theorem states that if a polynomial has a rational root, p q, then p is a factor of the constant term and q is a factor of the leading coefficient. Using the rational root theorem, state all the possible rational roots for the function. then, solve the function using synthetic division to check and find the actual roots of the function. Question: use rational roots theorem and find all rational roots of the following equation 80x3 42x2−35x 3=0. Use the rational root theorem to list all possible rational roots for the equation. then find any actual roots. x3 2x2 3x 6=0 a possible rational roots: 1,−1,2,−2,3,−3,6,−6. The overall strategy is to find the rational roots, and then to use factors based on the rational roots to reduce the polynomial degree by division. once we are working with a polynomial of degree one or two, we can use simple methods to find the remaining roots.

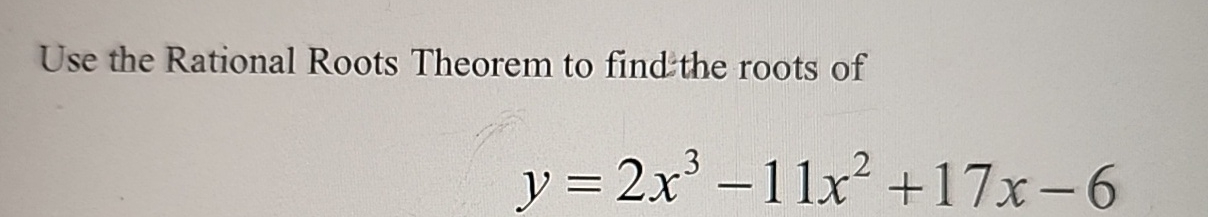
Use The Rational Roots Theorem To Find The Roots Chegg Using the rational root theorem, state all the possible rational roots for the function. then, solve the function using synthetic division to check and find the actual roots of the function. Question: use rational roots theorem and find all rational roots of the following equation 80x3 42x2−35x 3=0. Use the rational root theorem to list all possible rational roots for the equation. then find any actual roots. x3 2x2 3x 6=0 a possible rational roots: 1,−1,2,−2,3,−3,6,−6. The overall strategy is to find the rational roots, and then to use factors based on the rational roots to reduce the polynomial degree by division. once we are working with a polynomial of degree one or two, we can use simple methods to find the remaining roots.

From the moment you arrive, you'll be immersed in a realm of Solved Use Rational Roots Theorem And Find All Rational Chegg's finest treasures. Let your curiosity guide you as you uncover hidden gems, indulge in delectable delights, and forge unforgettable memories.

Rational Root Theorem

Rational Root Theorem

Rational Root Theorem Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem 20 - The Rational Root Theorem, Part 1 (Rational Roots of Polynomials) Rational Root Theorem (Rational Zero Theorem p/q) Rational Roots Theorem Determine all of the possible rational zeros of a polynomial Rational Root Theorem 2 (practice) Rational Root Theorem (Rational Zero Test to Find Zeros) Rational Roots Proof Using Rational Root Theorem 3.3 Rational Root Theorem Solving Equations Using the Rational Root Theorem Rational Roots Theorem(HD) How to Find Zeros of Polynomial Functions Ft. The Math Sorcerer Rational Roots Theorem Rational root theorem Proof of Rational Root Theorem Use the Rational Root Theorem to Find Rational Roots Rational Zeros Theorem Polynomial Equation Too Hard? Use THIS! (Rational Root Theorem)

Conclusion

Following an extensive investigation, it is obvious that write-up shares valuable understanding pertaining to Solved Use Rational Roots Theorem And Find All Rational Chegg. Across the whole article, the essayist exhibits substantial skill about the subject matter. Importantly, the section on underlying mechanisms stands out as extremely valuable. The presentation methodically addresses how these components connect to create a comprehensive understanding of Solved Use Rational Roots Theorem And Find All Rational Chegg.

Furthermore, the document is remarkable in clarifying complex concepts in an clear manner. This comprehensibility makes the information useful across different knowledge levels. The expert further elevates the presentation by inserting appropriate models and concrete applications that help contextualize the theoretical constructs.

A supplementary feature that sets this article apart is the detailed examination of several approaches related to Solved Use Rational Roots Theorem And Find All Rational Chegg. By examining these different viewpoints, the article delivers a well-rounded portrayal of the theme. The comprehensiveness with which the writer approaches the theme is truly commendable and sets a high standard for similar works in this domain.

In conclusion, this write-up not only informs the viewer about Solved Use Rational Roots Theorem And Find All Rational Chegg, but also encourages continued study into this fascinating theme. If you happen to be a novice or an authority, you will find worthwhile information in this extensive write-up. Thanks for reading this comprehensive post. Should you require additional details, feel free to connect with me by means of our contact form. I look forward to your comments. To expand your knowledge, you can see a few associated articles that are beneficial and enhancing to this exploration. Hope you find them interesting!