
Solved Using Calculus Show That Not All Goods Can Be Chegg Question: using calculus, show that not all goods can be inferior. (hint: start with the identity that y = p191 p2q2 pnqn.) dan dy dy dy dy o a. because = 1, at least one pi must be positive, which means at least one good, good i, is not inferior. dqi dy dqi because = 1, at least on dy dy dy 0 d. Using calculus, show that not all goods can be inferior. (hint: start with the identity that .y=p 1 q 1 p 2 q 2 … p n q n^*) cwatch the full video at:https:.

Solved Using Calculus Show That Not All Goods Can Be Chegg Using the total expenditure identity and calculus, we can show that if all goods were inferior, it would lead to a contradiction. since total expenditure's derivative indicates positive prices, at least one good must be normal, demonstrating that not all goods can be inferior. *2.5 using calculus, show that not all goods can be inferior . 4. suppose that we have a standard solow model with a cobb douglas production function. the central equation of the mode. in economics, we assume that preferences are monotonic, namely more is better. show using a figure with two goods that m. q4. Using calculus, show that not all goods can be inferior. (hint: start with the identity that y =p1q1 p2q2 … pnqn−1) define s n(x)= n 11 t n 1′ (x),n≥ 0, with t n 1(x) the chebyshev polynomial of degree n 1. the polynomials s n(x) are called chebyshev polynomials of the second kind. Using calculus, show that not all goods can be inferior. (hint: start with the identity that y p1q1 p2q2 pnqn ) dq1 da2 dan n dy dy note that p1 dy dy dy dy dy dy dy dy dy because 0, at least one must be positive, which means at least one good, good i, is not inferio. dy di dy although >, at least one can be negative, which means at least one.

Solved Calculus Chegg Using calculus, show that not all goods can be inferior. (hint: start with the identity that y =p1q1 p2q2 … pnqn−1) define s n(x)= n 11 t n 1′ (x),n≥ 0, with t n 1(x) the chebyshev polynomial of degree n 1. the polynomials s n(x) are called chebyshev polynomials of the second kind. Using calculus, show that not all goods can be inferior. (hint: start with the identity that y p1q1 p2q2 pnqn ) dq1 da2 dan n dy dy note that p1 dy dy dy dy dy dy dy dy dy because 0, at least one must be positive, which means at least one good, good i, is not inferio. dy di dy although >, at least one can be negative, which means at least one. About press copyright contact us creators advertise developers terms privacy policy & safety how works test new features nfl sunday ticket press copyright. Not all goods can be inferior because the income elasticity of demand for all goods combined, which equals 1, means the sum of negative elasticities (inferior goods) and positive elasticities (normal goods) must equal 1, implying not all can be negative. If the income effect more than offsets the substitution effect for a good, what do we call that good? 3.5 using a figure similar to figure 5.4 or that in solved *2.5 using calculus, show that not all goods can be inferior. Let $p$ and $q$ be integers with $q>0$. if $y=x^{p q}$, differentiate the equivalent equation $y^{q}=x^{p}$ implicitly and show that, for $y \neq 0….
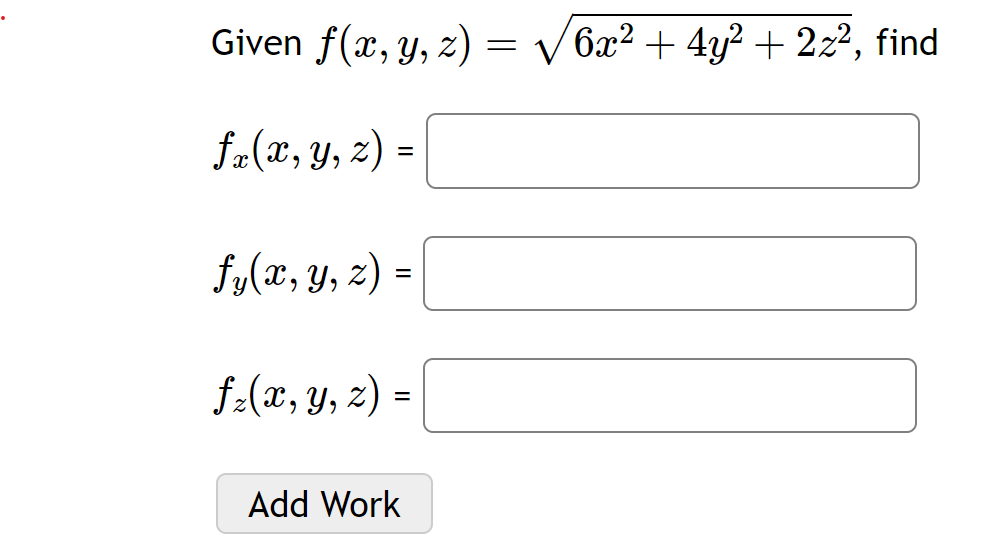
Calculus Chegg About press copyright contact us creators advertise developers terms privacy policy & safety how works test new features nfl sunday ticket press copyright. Not all goods can be inferior because the income elasticity of demand for all goods combined, which equals 1, means the sum of negative elasticities (inferior goods) and positive elasticities (normal goods) must equal 1, implying not all can be negative. If the income effect more than offsets the substitution effect for a good, what do we call that good? 3.5 using a figure similar to figure 5.4 or that in solved *2.5 using calculus, show that not all goods can be inferior. Let $p$ and $q$ be integers with $q>0$. if $y=x^{p q}$, differentiate the equivalent equation $y^{q}=x^{p}$ implicitly and show that, for $y \neq 0….
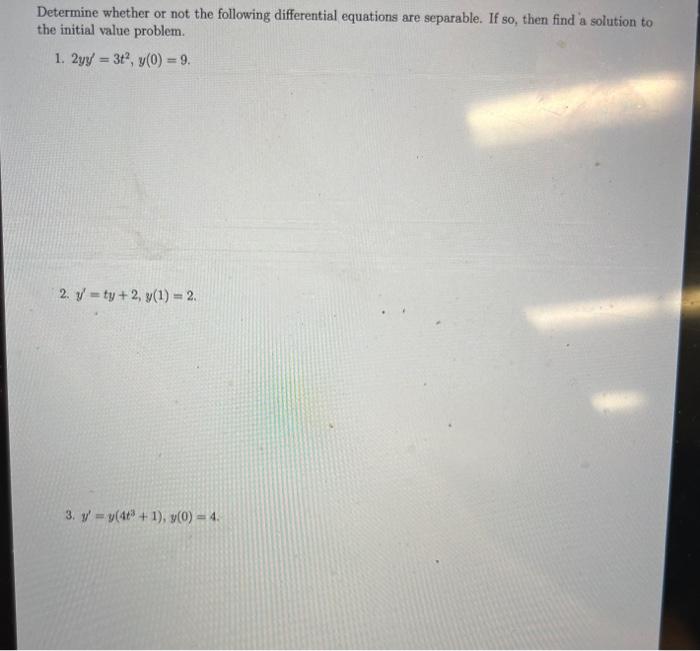
Solved Calculus Chegg If the income effect more than offsets the substitution effect for a good, what do we call that good? 3.5 using a figure similar to figure 5.4 or that in solved *2.5 using calculus, show that not all goods can be inferior. Let $p$ and $q$ be integers with $q>0$. if $y=x^{p q}$, differentiate the equivalent equation $y^{q}=x^{p}$ implicitly and show that, for $y \neq 0….
