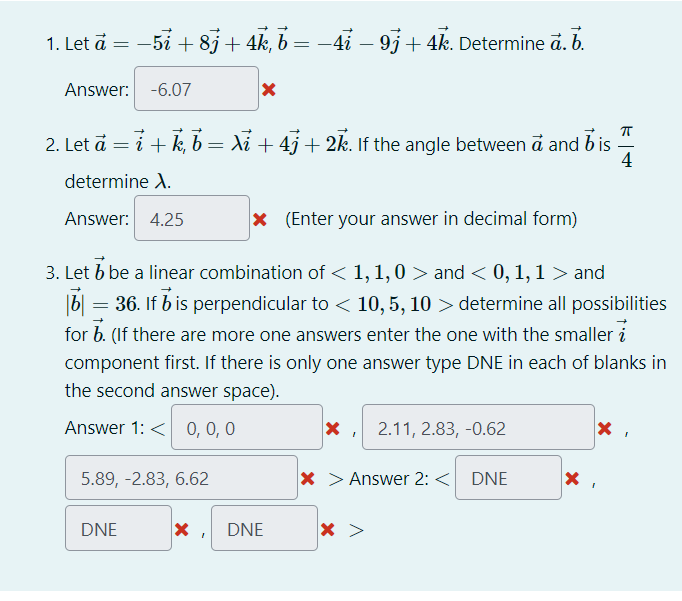
Solved 1 Let A тит5i 8j 4k B тит4iтит9j 4k Determine Aтлеb Chegg Answer to solved problems 5 8: let universal set u = { a, b, c, | chegg. Three important binary set operations are the union (u), intersection (∩), and cross product (x). a binary operation is called commutative if the order of the things it operates on doesn’t matter. for example, the addition ( ) operator over the integers is commutative, because for all possible integers x and y, x y = y x.
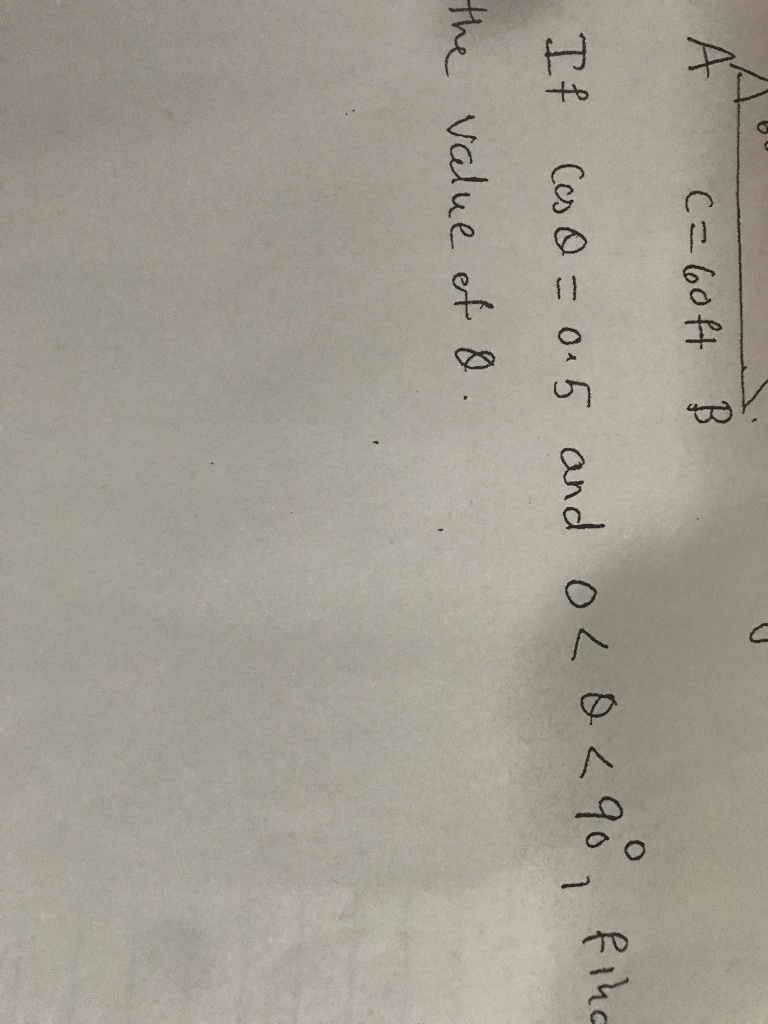
Solved Value Ef 8 Chegg Solution: (1) the three points (0;1), (1;0), (2;5) lying on the curve is equivalent to the following system of equations: 8 >< >: c= 1 a b c= 0 8a 2b c= 5, 2 4 0 0 1 1 1 1 8 2 1 3 5 2 4 a b c 3 5= 2 4 1 0 5 3 5 to solve this system, let’s put the matrix in reduced row echelon form: 2 4 0 0 1 1 1 1 1 0 8 2 1 5 3 5! switch rows 1 and 3 2 4. 1) dim(w 2)−dim(w 1 ∩w 2) 5. recall that a subspace w ⊆ v is t invariant for a linear transformation t, if t(w) ⊆ w. suppose that v = r(t)⊕w and that w is t invariant. prove that w ⊆ n(t). let w ∈ w. since w is t invariant, t(w) ∈ w. also, by definition, t(w) ∈ r(t), therefore t(w) ∈ r(t)∩w. Let u = { 1, 2, 3, 4, 5, 6, 7, 8, 9 } s = {1, 2, 5, 6, 7} t = {5, 6} v = {1, 2, 3, 5, 6, 9} find s′∪( t∩v) 22 – 33: on a standard 3 circle venn diagram, shade the region(s) corresponding to the. Let a and b be sets. the intersection of a and b (denoted by a ∩ b) is the set of all elements that are in both a and b. that is, a ∩ b = {x: x ∈ a and x ∈ b}. and b = {− 9, 22, 3}. b = {− 9, 22, 3}. then a ∩ b = {3}. a ∩ b = {3}. can be viewed as an intersection. let a = {(x, y): x y = 7, x, y ∈ r} a = {(x, y): x y = 7, x, y ∈ r}.

Solved Question 4let F X 8eï 2e2x 2 B 4x ï Where B E2then Chegg Let u = { 1, 2, 3, 4, 5, 6, 7, 8, 9 } s = {1, 2, 5, 6, 7} t = {5, 6} v = {1, 2, 3, 5, 6, 9} find s′∪( t∩v) 22 – 33: on a standard 3 circle venn diagram, shade the region(s) corresponding to the. Let a and b be sets. the intersection of a and b (denoted by a ∩ b) is the set of all elements that are in both a and b. that is, a ∩ b = {x: x ∈ a and x ∈ b}. and b = {− 9, 22, 3}. b = {− 9, 22, 3}. then a ∩ b = {3}. a ∩ b = {3}. can be viewed as an intersection. let a = {(x, y): x y = 7, x, y ∈ r} a = {(x, y): x y = 7, x, y ∈ r}. There are 2 steps to solve this one. given sets u = {a, b, c, d, e, f, g, h, i, j}, v = {a, e, i, f, h}, w = {a, c, e, g, i}. problems 5−8 : let universal set u ={a,b,c,d,e,f,g,h,i,j}, sets v ={a,e,i,f,h},w ={a,c,e,g,i} list the members of the following sets. 5) v∪w v ∪w 8) v ˉ ∩w ˉ. Solved problems on complement of a set are given below to get a fair idea how to find the complement of two or more sets. we know, when u be the universal set and a is a subset of u. then the complement of a is the set all elements of u which are not the elements of a. Let $a=\{1,2,\cdots,100\}$. for any $i \in \mathbb{n}$, define $a i$ as the set of numbers in $a$ that are divisible by $i$. for example: $$a 2=\{2,4,6,\cdots,100\},$$ $$a 3=\{3,6,9, \cdots, 99\}.$$ find $|a 2|$,$|a 3|$,$|a 4|$,$|a 5|$. find $|a 2 \cup a 3 \cup a 5|$. In this article, we have learned about the universal set, its complement and subsets. let’s solve some universal set examples and practice problems for better understanding. solved examples on universal set. 1. assuming p is the set of positive odd integers and q is the set of positive even integers, write the universal set of p and q. solution:.

Solved 8 14 E B с Chegg There are 2 steps to solve this one. given sets u = {a, b, c, d, e, f, g, h, i, j}, v = {a, e, i, f, h}, w = {a, c, e, g, i}. problems 5−8 : let universal set u ={a,b,c,d,e,f,g,h,i,j}, sets v ={a,e,i,f,h},w ={a,c,e,g,i} list the members of the following sets. 5) v∪w v ∪w 8) v ˉ ∩w ˉ. Solved problems on complement of a set are given below to get a fair idea how to find the complement of two or more sets. we know, when u be the universal set and a is a subset of u. then the complement of a is the set all elements of u which are not the elements of a. Let $a=\{1,2,\cdots,100\}$. for any $i \in \mathbb{n}$, define $a i$ as the set of numbers in $a$ that are divisible by $i$. for example: $$a 2=\{2,4,6,\cdots,100\},$$ $$a 3=\{3,6,9, \cdots, 99\}.$$ find $|a 2|$,$|a 3|$,$|a 4|$,$|a 5|$. find $|a 2 \cup a 3 \cup a 5|$. In this article, we have learned about the universal set, its complement and subsets. let’s solve some universal set examples and practice problems for better understanding. solved examples on universal set. 1. assuming p is the set of positive odd integers and q is the set of positive even integers, write the universal set of p and q. solution:.

Solved If F 8 4 F 8 5 G 8 3 G 8 1 And Chegg Let $a=\{1,2,\cdots,100\}$. for any $i \in \mathbb{n}$, define $a i$ as the set of numbers in $a$ that are divisible by $i$. for example: $$a 2=\{2,4,6,\cdots,100\},$$ $$a 3=\{3,6,9, \cdots, 99\}.$$ find $|a 2|$,$|a 3|$,$|a 4|$,$|a 5|$. find $|a 2 \cup a 3 \cup a 5|$. In this article, we have learned about the universal set, its complement and subsets. let’s solve some universal set examples and practice problems for better understanding. solved examples on universal set. 1. assuming p is the set of positive odd integers and q is the set of positive even integers, write the universal set of p and q. solution:.
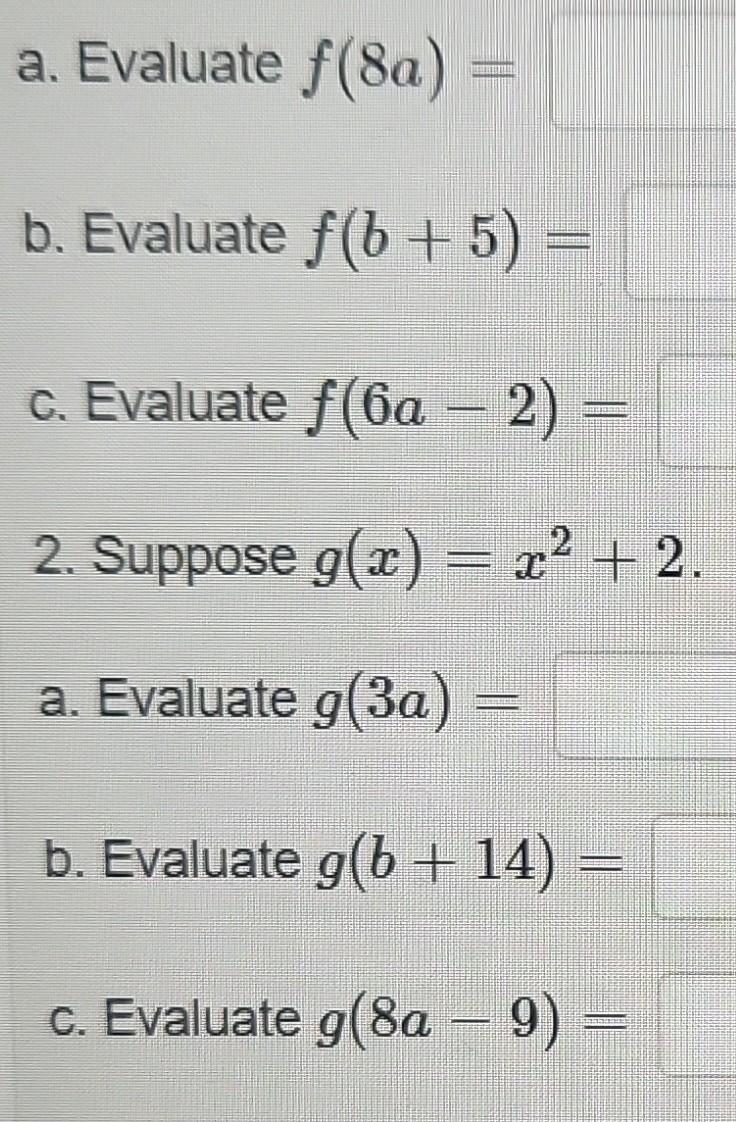
Solved A Evaluate F 8a B Evaluate F B 5 C Evaluate Chegg
