
Absolute Conditional Convergence Calculus 2 Definition 3.4.1 absolute and conditional convergence a series \(\sum\limits {n=1}^\infty a n\) is said to converge absolutely if the series \(\sum\limits {n=1}^\infty |a n|\) converges. if \(\sum\limits {n=1}^\infty a n\) converges but \(\sum\limits {n=1}^\infty |a n|\) diverges we say that \(\sum\limits {n=1}^\infty a n\) is conditionally. What is conditional convergence? conditional convergence occurs in an infinite series when the series converges, but it does not converge absolutely. in other words, the series ∑a n converges, but the series formed by taking the absolute values of its terms, ∑∣a n ∣, diverges.

Solved What Is Difference Between Absolute Convergence And Chegg In this section we will have a brief discussion on absolute convergence and conditionally convergent and how they relate to convergence of infinite series. In this article, we study absolute and conditional convergence with their definitions and examples. definition: a series ∑ n = 1 ∞ a n is called absolutely convergent if the series ∑ n = 1 ∞ | a n | is convergent. for example, the series 1 − 1 2 2 1 3 2 − 1 4 2 ⋯ is an absolutely convergent series. an absolutely convergent series is convergent. Absolute convergence is a concept in mathematics that pertains to the convergence of an infinite series. specifically, a series \sum {n=1}^ {\infty} a n ∑n=1∞ an is said to converge absolutely if the series of the absolute values of its terms, \sum {n=1}^ {\infty} a n ∑n=1∞ an, also converges. In summary, absolute convergence is a stronger condition, ensuring the series converges regardless of term signs, while conditional convergence relies on the alternating nature of the series and can fail if the terms are not arranged correctly.
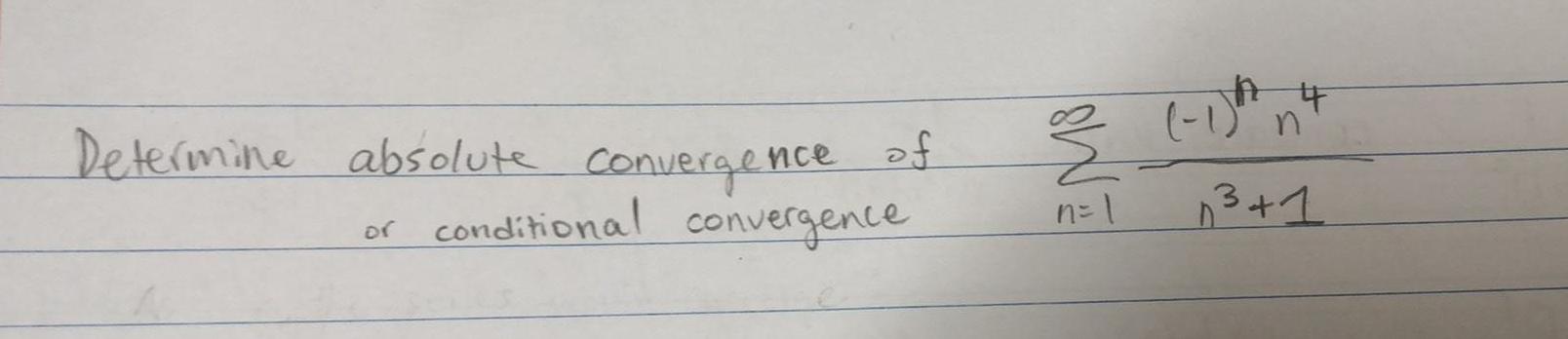
Answered Determine Absolute Or Convergence Of Conditional Convergence Absolute convergence is a concept in mathematics that pertains to the convergence of an infinite series. specifically, a series \sum {n=1}^ {\infty} a n ∑n=1∞ an is said to converge absolutely if the series of the absolute values of its terms, \sum {n=1}^ {\infty} a n ∑n=1∞ an, also converges. In summary, absolute convergence is a stronger condition, ensuring the series converges regardless of term signs, while conditional convergence relies on the alternating nature of the series and can fail if the terms are not arranged correctly. Here’s an example. determine the convergence or divergence of the following alternating series: if all these terms were positive, you’d have the familiar geometric series, which, by the geometric series rule, converges to 2. One unique thing about series with positive and negative terms (including alternating series) is the question of absolute or conditional convergence. once convergence of the series is established, then determining the convergence of the absolute value of the series tells you whether it converges absolutely or conditionally. To decide whether it converges absolutely, we look at the series of absolute values, x∞ k=1 1 √ k. this is a p series with p = 1 2, and we know that diverges. so, x∞ k=1 (−1)k √ k converges conditionally . (b) x∞ k=1 sink k!. solution. this series is not an alternating series, so we should not even try the alternating series test. In this review article, we’ll take a look at the difference between absolute and conditional convergence. along the way, we’ll see a few examples and discuss important special cases. if a series has a finite sum, then the series converges. otherwise, the series diverges.
