
Completing The Square Practice Worksheet Worksheets Library Solving general quadratic equations by completing the square. we can complete the square to solve a quadratic equation (find where it is equal to zero). but a general quadratic equation may have a coefficient of a in front of x 2: ax 2 bx c = 0. to deal with that we divide the whole equation by "a" first, then carry on: x 2 (b a)x c a. In this section, we will solve quadratic equations by a process called completing the square, which is important for our work on conics later. in the last section, we were able to use the square root property to solve the equation (y − 7)2 = 12 (y − 7) 2 = 12 because the left side was a perfect square.

Solving Quadratic Equations By Completing The Square Ppt Tessshebaylo Solve quadratic equations by factorising, using formulae and completing the square. each method also provides information about the corresponding quadratic graph. some quadratics cannot. Completing the square is a method in mathematics that is used for converting a quadratic expression of the form ax 2 bx c to the vertex form a(x m) 2 n. the most common use of this method is in solving a quadratic equation which can be done by rearranging the expression obtained after completing the square. Learn how to solve the quadratic equations by the method of completing the square with formula, steps, examples, and diagram. Learn how to use the technique of completing the square to rearrange a quadratic equation into a perfect square and solve it by taking the square root of both sides. follow the step by step example with detailed explanations and diagrams.

Math Example Quadratics Completing The Square Example 7 Worksheets Learn how to solve the quadratic equations by the method of completing the square with formula, steps, examples, and diagram. Learn how to use the technique of completing the square to rearrange a quadratic equation into a perfect square and solve it by taking the square root of both sides. follow the step by step example with detailed explanations and diagrams. The completing the square practice tool helps students master solving quadratic equations by completing the square through six interactive questions, covering easy to difficult levels. students enter solutions in the correct format (e.g., ) and receive instant feedback. correct answers are marked with a green check ( ), while incorrect answers. Demonstrates how to solve quadratics by completing the square, provides a link to a page showing how to "prove" the quadratic formula using this method, and recommends against using this solution technique unless required to do so. Solve quadratic equations of the form ax 2 bx c = 0 by completing the square. the process of completing the square works best when the coefficient of x 2 is 1, so the left side of the equation is of the form x 2 bx c. if the x 2 term has a coefficient other than 1, we take some preliminary steps to make the coefficient equal to 1. Learn how to solve quadratic equations using the completing the square method with seven (7) easy worked examples.
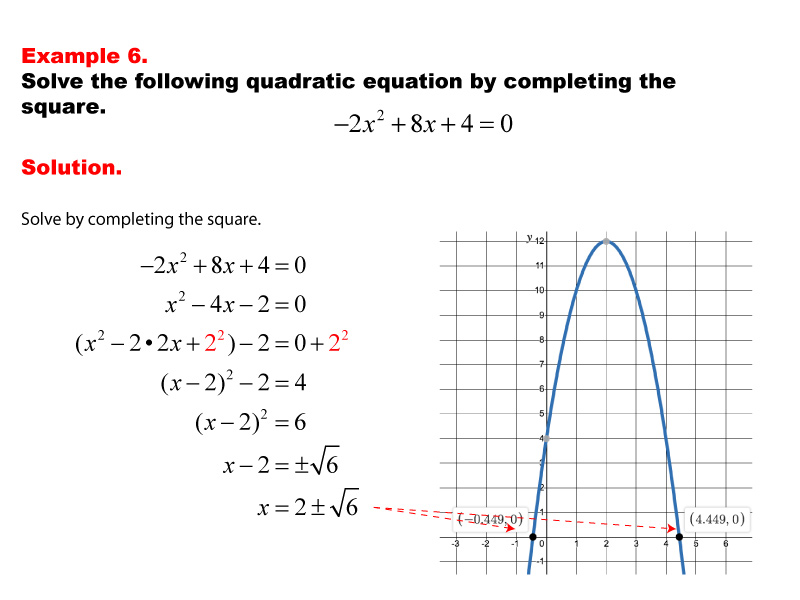
Student Tutorial Solving Quadratic Equations In Standard Form By The completing the square practice tool helps students master solving quadratic equations by completing the square through six interactive questions, covering easy to difficult levels. students enter solutions in the correct format (e.g., ) and receive instant feedback. correct answers are marked with a green check ( ), while incorrect answers. Demonstrates how to solve quadratics by completing the square, provides a link to a page showing how to "prove" the quadratic formula using this method, and recommends against using this solution technique unless required to do so. Solve quadratic equations of the form ax 2 bx c = 0 by completing the square. the process of completing the square works best when the coefficient of x 2 is 1, so the left side of the equation is of the form x 2 bx c. if the x 2 term has a coefficient other than 1, we take some preliminary steps to make the coefficient equal to 1. Learn how to solve quadratic equations using the completing the square method with seven (7) easy worked examples.
