Solving Quadratic Equations By Graphing
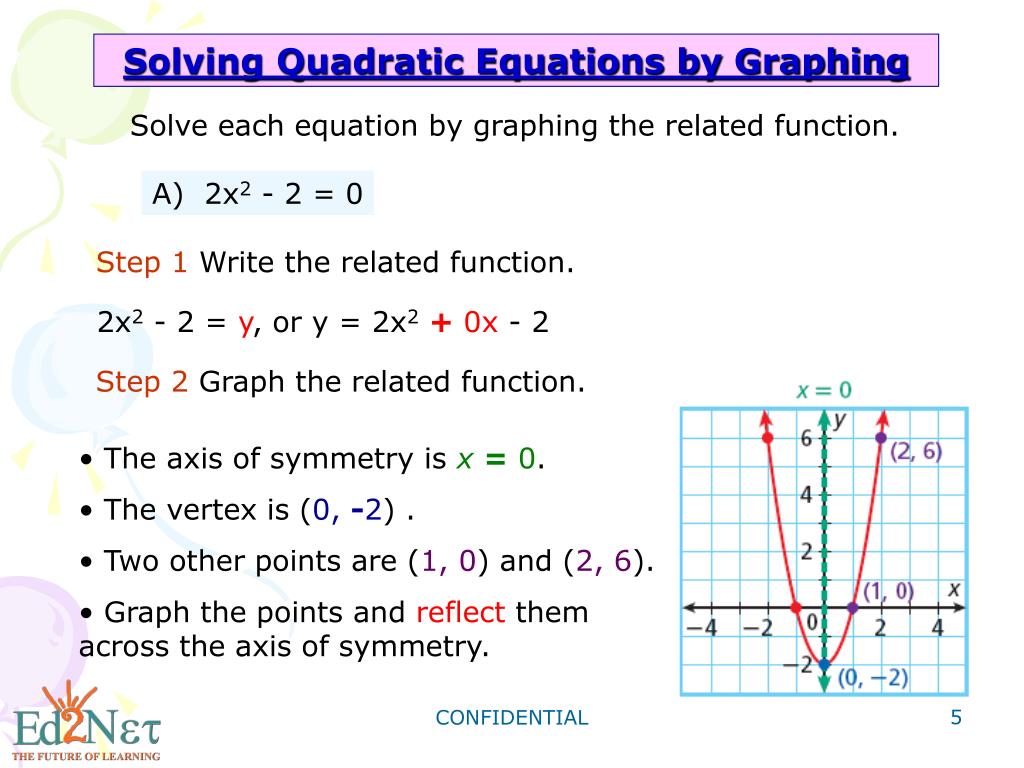
Ppt Solving Quadratic Equations By Graphing Powerpoint Presentation The solutions to a quadratic equation are also called the roots or zeros of the function, and in this section we'll learn how to find them by graphing the function. Learn how to graph quadratic equations using the general form f(x) = a(x h)^2 k, where h and k are the vertex and y intercept of the parabola. see examples, tips, and interactive explorers to practice graphing quadratic equations.

Solving Quadratic Equations By Graphing Examples Practice Expii Learn how to find the roots of a quadratic equation by using its graph, which is a parabola. see examples, definitions, and worksheets for solving quadratic equations by graphing in high school algebra. Learn how to find the roots of a quadratic equation by graphing it and comparing it to the x intercepts. see examples, worksheets and a video lesson on solving quadratic equations graphically. Learn how to use the graph of a quadratic function to find the zeros of the equation. see examples of different types of zeros, such as real roots, double roots, and rational roots, and how to estimate solutions to a problem. Solving quadratic equations by graphing estimate solutions the roots of a. quadratic equation may not be integers. if exact roots cannot be found, they can be estimated by finding the consecuti. e integers between which the roots lie. ex.
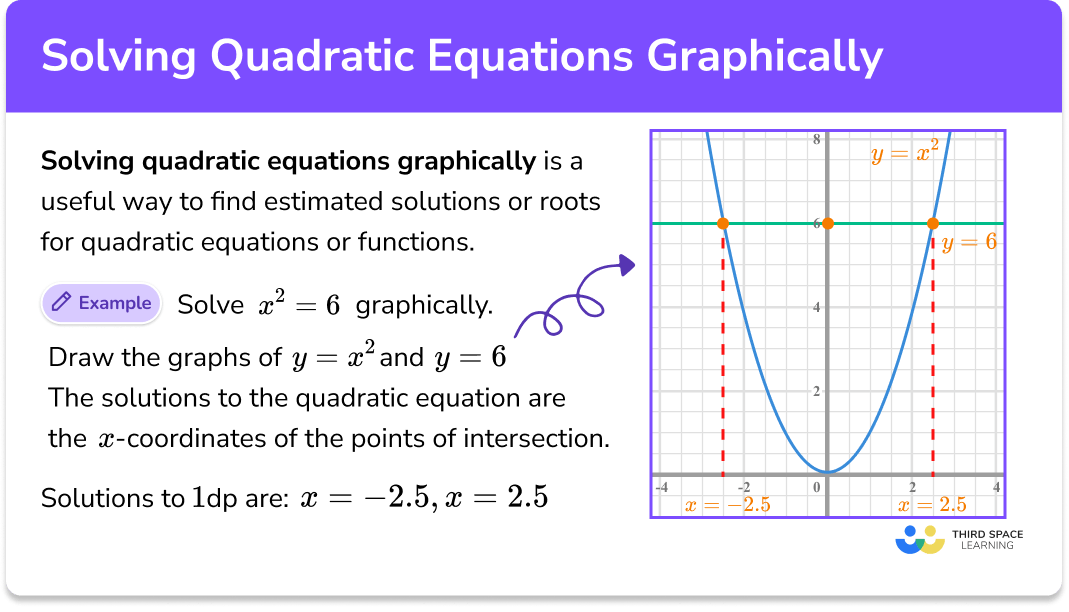
Solving Quadratic Equations By Graphing Worksheets Printable Online Learn how to use the graph of a quadratic function to find the zeros of the equation. see examples of different types of zeros, such as real roots, double roots, and rational roots, and how to estimate solutions to a problem. Solving quadratic equations by graphing estimate solutions the roots of a. quadratic equation may not be integers. if exact roots cannot be found, they can be estimated by finding the consecuti. e integers between which the roots lie. ex. We need to locate the parabola's x intercepts. these are our solutions. the x intercepts are located where the parabola crosses the x axis. in our graph, the parabola crosses the x axis at x=−5 and x=1. so, the solution to the quadratic equation is: x=−5,1. by textbook tactics. We can graph the equation using the table of points in the previous example to see where the graph passes through y = 3. notice that a quadratic equation graphs a parabola shape, not a line, because squaring creates two possible solutions, as we saw from our guess and check work. the graph below shows the solution to happens at (1,3) and (5,3). Learn how to solve quadratic equations using graphs. this step by step guide explains how to identify solutions by finding. Learn how to use the standard form of a quadratic equation to graph it and find the x intercepts, which are the solutions of the equation. see examples, key concepts, and guided practice problems with solutions and graphs.
Comments are closed.