Solving Trigonometric Equations Using Identities Multiple Angles By Factoring General Solution

Trigonometric Identities And Equations Pdf Trigonometric Functions Step by step tutorial explains how to solve trigonometric equations with multiple angles. ace your math exam!. Using algebra techniques and knowledge of the unit circle to solve trigonometric equations write an equation to represent all possible solutions of a trigonometric equation by accounting for coterminal angles.

Solving Trigonometric Equations Using Factoring Tessshebaylo Given a trigonometric equation, solve using algebra. look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity. solve the equation the same way an algebraic equation would be solved. substitute the trigonometric expression back in for the variable in the resulting expressions. With these types of functions, we use algebraic techniques like factoring, the quadratic formula, and trigonometric identities to break the equation down to equations that are easier to work with. The equations in examples 1 and 2 involved only one trigonometric function. when two or more functions occur in the same equation, collect all terms on one side and try to separate the functions by factoring or by using appropriate identities. Using an identity, we can rewrite the equation and solve it. this is the original equation. combine like terms. next, set each factor equal to 0 and solve. set the first factor equal to 0. set the second factor equal to 0. add to both sides and write on the left side.

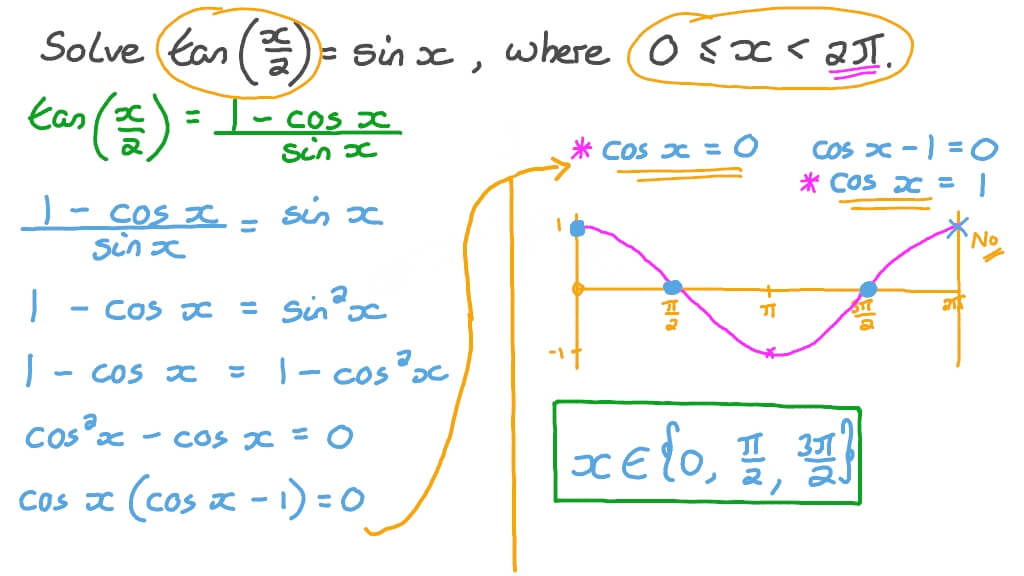
Solving Trigonometric Equations Using Factoring Tessshebaylo The equations in examples 1 and 2 involved only one trigonometric function. when two or more functions occur in the same equation, collect all terms on one side and try to separate the functions by factoring or by using appropriate identities. Using an identity, we can rewrite the equation and solve it. this is the original equation. combine like terms. next, set each factor equal to 0 and solve. set the first factor equal to 0. set the second factor equal to 0. add to both sides and write on the left side. We will begin with the pythagorean identities, which are equations involving trigonometric functions based on the properties of a right triangle. we have already seen and used the first of these identifies, but now we will also use additional identities. In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions. The formulas that result from letting u = v in the angle sum identities are called the double angle identities. we will state them all and prove one, leaving the rest of the proofs as exercises.

Solving Trigonometric Equations Using Factoring Tessshebaylo We will begin with the pythagorean identities, which are equations involving trigonometric functions based on the properties of a right triangle. we have already seen and used the first of these identifies, but now we will also use additional identities. In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions. The formulas that result from letting u = v in the angle sum identities are called the double angle identities. we will state them all and prove one, leaving the rest of the proofs as exercises.

Solving Trigonometric Equations Using Identities Worksheet Tessshebaylo The formulas that result from letting u = v in the angle sum identities are called the double angle identities. we will state them all and prove one, leaving the rest of the proofs as exercises.

Solving Trigonometric Equations Using Identities Worksheet Tessshebaylo