State If The Two Vectors Are Parallel Orthogonal Or Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. check if th not the question you’re looking for? post any question and get expert help quickly. Parallel and orthogonal vectors definition: parallel vectors two vectors \ (\vec {u}=\left\langle u x, u y\right\rangle\) and \ (\vec {v}=\left\langle v x, v y\right\rangle\) are parallel if the angle between them is \ (0^ {\circ}\) or \ (180^ {\circ}\).
Solved State If The Two Vectors Are Parallel Orthogonal Or Chegg Let's determine if the given pairs of vectors are parallel, orthogonal, or neither. parallel vectors: two vectors are parallel if they are scalar multiples of each other. in a 2d space, this is true if the cross product of the vectors is zero or if their ratios (component wise) are the same. You can setermine whether two vectors are parallel, orthogonal, or neither uxsing the dot cross product or using the slope formula. We know we can check if two vectors are 'orthogonal' by doing an inner product. $a*b=0$ tells us that these two vectors are orthogonal. here comes the question: if there a way to compute if they are 'parallel'? i.e., they are pointing at the same direction. State whether the vectors are parallel, orthogonal, or neither. to determine whether two vectors are parallel, orthogonal, or neither, we can use the dot product and the properties of the vectors. here, a = 3, b = −1, c = 6, and d = −2. two vectors are orthogonal if their dot product is zero.
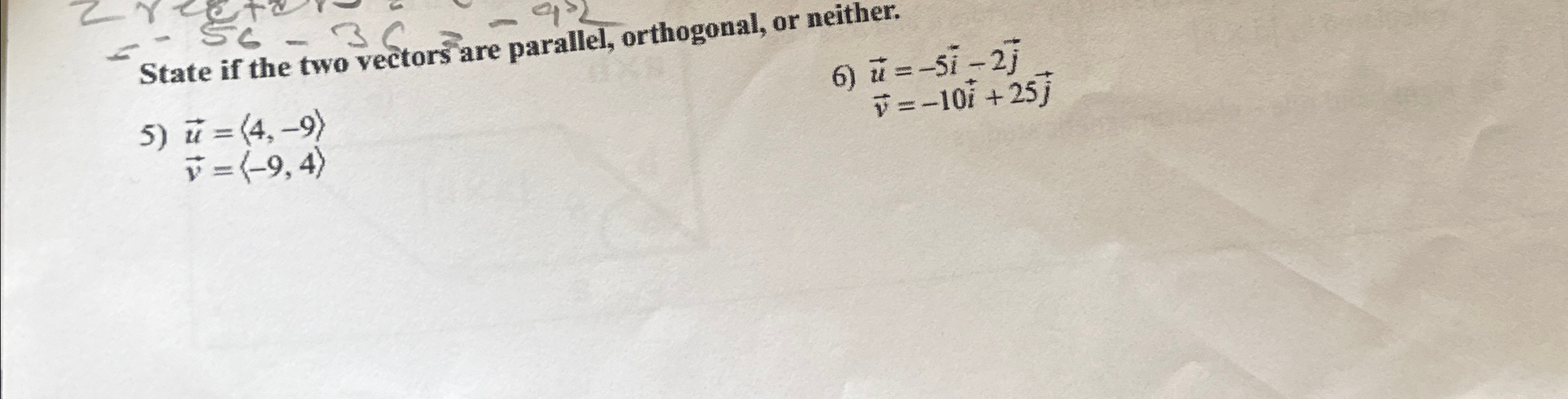
Solved State If The Two Vectors Are Parallel Orthogonal Or Chegg We know we can check if two vectors are 'orthogonal' by doing an inner product. $a*b=0$ tells us that these two vectors are orthogonal. here comes the question: if there a way to compute if they are 'parallel'? i.e., they are pointing at the same direction. State whether the vectors are parallel, orthogonal, or neither. to determine whether two vectors are parallel, orthogonal, or neither, we can use the dot product and the properties of the vectors. here, a = 3, b = −1, c = 6, and d = −2. two vectors are orthogonal if their dot product is zero. Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. That's right, and to check being parallel, you'd check to see if the left hand side expression was 1.0, rather than 0.0. that is you'd see if the difference from 1.0 was less than epsilon. Next, we assumed that some constant c c c existed such that a = c b \bold {a}=c\bold {b} a=cb. two vectors were equal if the corresponding components were equal. this gave us a system of equations, which we solved to c c c. if this system had a solution c c c, then the vectors were parallel. Since the vectors are neither parallel nor orthogonal, they are neither. check for parallelism.
Comments are closed.