State Whether The Equation X 1 X 2 X 0 Has Two Distinct Real

State Whether The Equation X 1 X 2 X 0 Has Two Distinct Real We know that a quadratic equation ax² bx c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero. therefore, the equation has 2 distinct real roots. So, given equation has two distinct real roots. state whether the equation (x 1) (x 2) x = 0 has two distinct real roots or not. justify your answer.

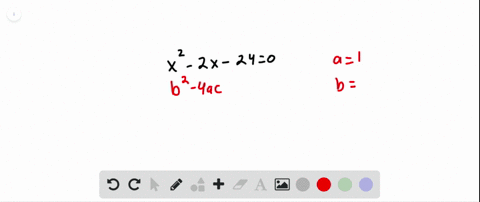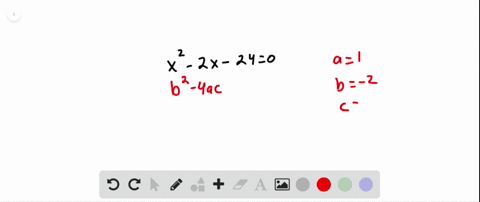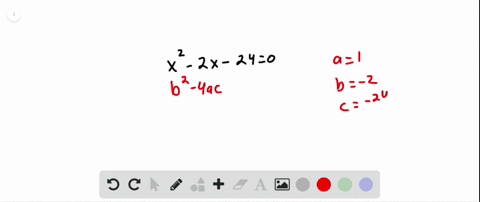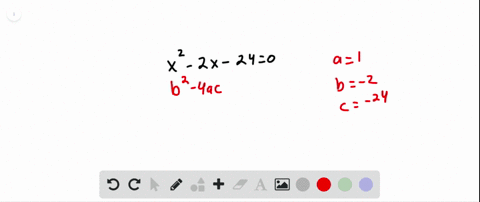
Solved Tell Whether The Equation Has Two Solutions One Solution Or No To determine if the quadratic equation x (1 x) 2 = 0 has two distinct real roots, we need to find the discriminant (Δ) of the equation. first, let's rewrite the equation in standard quadratic form a x 2 b x c = 0. The equation x (1 – x) – 2 = 0 has no real roots. simplifying the above equation, x 2 – x 2 = 0 d = b 2 – 4ac = (–1) 2 – 4 (1) (2) = 1 – 8 < 0 hence, the roots are imaginary. We want $\delta$ to be always positive, then the given equation will always have two distinct real roots. for this to happen, the discriminant of $\delta$ must be negative. Explicit examples of quadratic equations would include \ (x^2 3x 2 = (x 1) (x 2) = 0\), which has two distinct real roots, and \ (x^2 1=0\), which has no real roots.

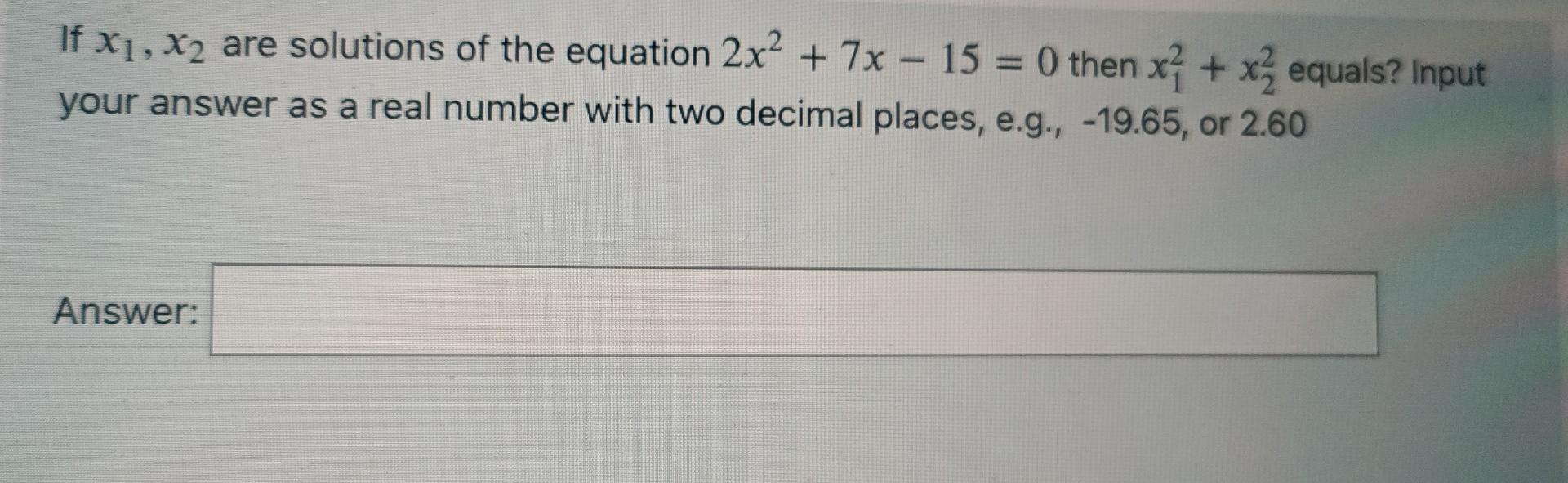
Solved If X1 X2 Are Solutions Of The Equation 2x2 7x 15 0 Chegg We want $\delta$ to be always positive, then the given equation will always have two distinct real roots. for this to happen, the discriminant of $\delta$ must be negative. Explicit examples of quadratic equations would include \ (x^2 3x 2 = (x 1) (x 2) = 0\), which has two distinct real roots, and \ (x^2 1=0\), which has no real roots. To determine which of the given quadratic equations has two distinct real roots, we need to use the concept of the discriminant. the discriminant d of a quadratic equation in the form ax2 bx c =0 is given by the formula:. The equation (x – 1) (x 2) 2 = 0 has two real and distinct roots. simplifying the above equation, x2 – x 2x – 2 2 = 0 x2 x = 0 d = b2 – 4ac = 12 – 4 (1) (0) = 1 – 0 > 0 hence, the roots are real and distinct. We know that a quadratic equation ax² bx c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero. therefore, the equation has 2 distinct real roots. To determine if the quadratic equation has two distinct real roots, we need to find the discriminant (d) of the equation. the discriminant is given by the formula:.

Solved Determine Whether The Equation Has Two Solutions One Solution To determine which of the given quadratic equations has two distinct real roots, we need to use the concept of the discriminant. the discriminant d of a quadratic equation in the form ax2 bx c =0 is given by the formula:. The equation (x – 1) (x 2) 2 = 0 has two real and distinct roots. simplifying the above equation, x2 – x 2x – 2 2 = 0 x2 x = 0 d = b2 – 4ac = 12 – 4 (1) (0) = 1 – 0 > 0 hence, the roots are real and distinct. We know that a quadratic equation ax² bx c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero. therefore, the equation has 2 distinct real roots. To determine if the quadratic equation has two distinct real roots, we need to find the discriminant (d) of the equation. the discriminant is given by the formula:.