
Stirlings Approximation Solved Pdf Mathematical Objects The main idea of why the stirling formula looks like this.the rest is only to show how does the n! [ (n e)^n*sqrt (n)] acts,but the fact that it is bounded fro. For this reason it is quite intriguing that a rough approximation of the stirling formula for the asymptotic behavior of ln( n !) is commonly used, namely the stirling approxi mation: ln( n !) ≃ n ln( n e ).

Stirling S Approximation To N How do the two most important fundamental constants of mathematics, e and π, find their way into an asymptotic formula for the product of integers? we give two very different arguments (one will not show the full formula) that, between them, illustrate a good number of basic asymptotic methods. Stirling’s formula keith conrad 1. introduction our goal is to prove the following asymptotic estimate for n!, called stirling’s formula. theorem 1.1. as n!1, n! ˘ nn en p 2ˇn. that is, lim n!1 n! (nn=en) p 2ˇn = 1. example 1.2. set n= 10: 10! = 3628800 and (1010=e10) p 2ˇ(10) = 3598695:61:::. the. Consider stirling's approximation. n! = √2πn(n e)n(1 o(1 n)) lim n → ∞ n! √2πn(n e)n = 1 the exact terms of the expression are more precisely described by stirling's series. Another approach to stirling’s formula involves writing (3.1) log¡(z) = ‡ z ¡ 1 2 · logz ¡ z 1 2 log2… !(z); with a convenient integral formula for!(z). this is done in x12.33 of [ww], and, to even better efiect, in x1.4 of [leb], which obtains (3.2)!(z) = z 1 0 f(t)e¡tz dt; with (3.3) f(t) = ‡1 2 ¡ 1 t 1 et ¡ 1 ·1 t;.
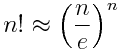
Simpler Version Of Stirling S Approximation Consider stirling's approximation. n! = √2πn(n e)n(1 o(1 n)) lim n → ∞ n! √2πn(n e)n = 1 the exact terms of the expression are more precisely described by stirling's series. Another approach to stirling’s formula involves writing (3.1) log¡(z) = ‡ z ¡ 1 2 · logz ¡ z 1 2 log2… !(z); with a convenient integral formula for!(z). this is done in x12.33 of [ww], and, to even better efiect, in x1.4 of [leb], which obtains (3.2)!(z) = z 1 0 f(t)e¡tz dt; with (3.3) f(t) = ‡1 2 ¡ 1 t 1 et ¡ 1 ·1 t;. Where does stirling’s approximation \(n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n\) come from? well, \(n! = \prod {t = 1}^{n} t\), a discrete product. one obvious way to try to approximate a solution for \(n!\) is to switch from discrete series to continuous series. Stirling approximation says n! 2 n (ne)n as n ! 1 in the asymptotic sense that the ratio has limit 1. Idea. stirling’s approximation, or stirling’s formula, gives an asymptotic approximation to the factorial function in terms of elementary functions. statement. define n! n! for n ∈ ℕ n \in \mathbb{n} as usual by recursion: 0! = 1 0! = 1 and (n 1)! = (n 1) ⋅ n! (n 1)! = (n 1) \cdot n!. stirling’s approximation says.
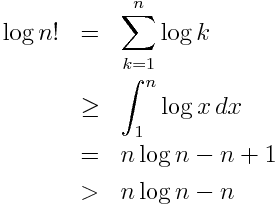
Simpler Version Of Stirling S Approximation Where does stirling’s approximation \(n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n\) come from? well, \(n! = \prod {t = 1}^{n} t\), a discrete product. one obvious way to try to approximate a solution for \(n!\) is to switch from discrete series to continuous series. Stirling approximation says n! 2 n (ne)n as n ! 1 in the asymptotic sense that the ratio has limit 1. Idea. stirling’s approximation, or stirling’s formula, gives an asymptotic approximation to the factorial function in terms of elementary functions. statement. define n! n! for n ∈ ℕ n \in \mathbb{n} as usual by recursion: 0! = 1 0! = 1 and (n 1)! = (n 1) ⋅ n! (n 1)! = (n 1) \cdot n!. stirling’s approximation says.
