
Stirlings Approximation Solved Pdf Mathematical Objects Stirling's approximation gives an approximate value for the factorial function n! or the gamma function gamma (n) for n>>1. the approximation can most simply be derived for n an integer by approximating the sum over the terms of the factorial with an integral, so that lnn! = ln1 ln2 lnn (1) = sum (k=1)^ (n)lnk (2) approx int 1^nlnxdx (3. See also bernoulli number, gamma function, k function, log gamma function, permutation cycle, stirling's approximation explore with wolfram|alpha.
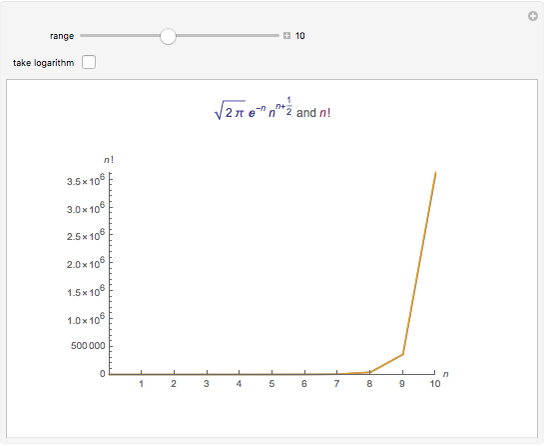
Stirling S Approximation Versus N Wolfram Demonstrations Project About mathworld mathworld classroom contribute mathworld book 13,256 entries last updated: fri apr 18 2025 ©1999–2025 wolfram research, inc. terms of use wolfram wolfram for education created, developed and nurtured by eric weisstein at wolfram research. In mathematics, stirling's approximation (or stirling's formula) is an asymptotic approximation for factorials. it is a good approximation, leading to accurate results even for small values of . Wolfram language function: compute an approximation to a factorial with stirling's formula. complete documentation and usage examples. download an example notebook or open in the cloud. We have the identity n! = Γ(n 1) = ∫∞ 0 tne−tdt n! = Γ (n 1) = ∫ 0 ∞ t n e − t d t. from this point of view, the point of stirling's approximation is that tne−t t n e − t attains its maximum at t = n t = n, so we expect that this is where the main contribution to the integral comes from.
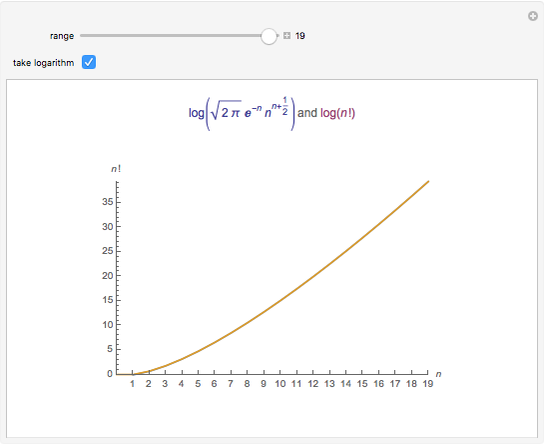
Stirling S Approximation Versus N Wolfram Demonstrations Project Wolfram language function: compute an approximation to a factorial with stirling's formula. complete documentation and usage examples. download an example notebook or open in the cloud. We have the identity n! = Γ(n 1) = ∫∞ 0 tne−tdt n! = Γ (n 1) = ∫ 0 ∞ t n e − t d t. from this point of view, the point of stirling's approximation is that tne−t t n e − t attains its maximum at t = n t = n, so we expect that this is where the main contribution to the integral comes from. Stirling's approximation is a method of approximating a factorial n!. as the value of n increases, the more exact the approximation becomes; however, it still yields almost exact results for small values of n. Basestyle >"hyperlink", buttondata:>{ url[" mathworld.wolfram notebooks calculus \ stirlingsapproximation.nb"], none}], "." }], "text"], cell[textdata[{ "for more information, see eric's ", stylebox["mathworld", fontslant >"italic"], " entry ", buttonbox[" mathworld.wolfram stirlingsapproximation ",. Stirling approximation : a function that approximates factorials. n! is defined as n * (n 1) * (n 2) * (n 3) …. but have you ever heard of the function called the stirling. This essay summarizes the importance of the stirling approximation and finds that it is a fundamental calculation method for explaining and solving thermodynamics related problems which can be used in various subtopics and fields.
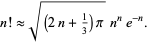
Stirling S Approximation From Wolfram Mathworld Stirling's approximation is a method of approximating a factorial n!. as the value of n increases, the more exact the approximation becomes; however, it still yields almost exact results for small values of n. Basestyle >"hyperlink", buttondata:>{ url[" mathworld.wolfram notebooks calculus \ stirlingsapproximation.nb"], none}], "." }], "text"], cell[textdata[{ "for more information, see eric's ", stylebox["mathworld", fontslant >"italic"], " entry ", buttonbox[" mathworld.wolfram stirlingsapproximation ",. Stirling approximation : a function that approximates factorials. n! is defined as n * (n 1) * (n 2) * (n 3) …. but have you ever heard of the function called the stirling. This essay summarizes the importance of the stirling approximation and finds that it is a fundamental calculation method for explaining and solving thermodynamics related problems which can be used in various subtopics and fields.
