
Stirlings Approximation Solved Pdf Mathematical Objects We prove stirling's formula that approximates n! using laplace's method. get my favorite, free calculator app for your phone or tablet: maple calculator: htt. In mathematics, stirling's approximation (or stirling's formula) is an asymptotic approximation for factorials. it is a good approximation, leading to accurate results even for small values of . it is named after james stirling, though a related but less precise result was first stated by abraham de moivre. [1][2][3].

Solved 1 59 We Can Derive Stirling S Approximation Form An Chegg Starting with euler’s integral definition of the gamma function, we state and prove the bohr–mollerup theorem, which gives euler’s limit formula for the gamma func tion. we then discuss two independent topics. the first is upper and lower bounds on the gamma function, which lead to stirling’s formula. James stirling (scottish mathematician, 1692 1770) presented a way to estimate it with enough accuracy. − n ( ! p ! n p ) ! − n ( ! p ! n p ) ! n = ! ) p − n ( ! p p. ln w ( m , n ) = ln n ! p !. Laplace’s approach to stirling’s formula is noteworthy first, because it makes a direct connection with the gaussian (normal) distribution (whereas in other approaches the gaussian distribution enters indirectly, or not at all), and second, because it provides a general. We could get (15) from laplace’s method by using more terms in the expansion around zero, but this would involve long calculations, and there are much better ways (beyond the scope of this course though). the approximation by a truncated expansion gets more and more accurate as ngrow. but even for n= 5, using only the rst 4 terms we get 5!.
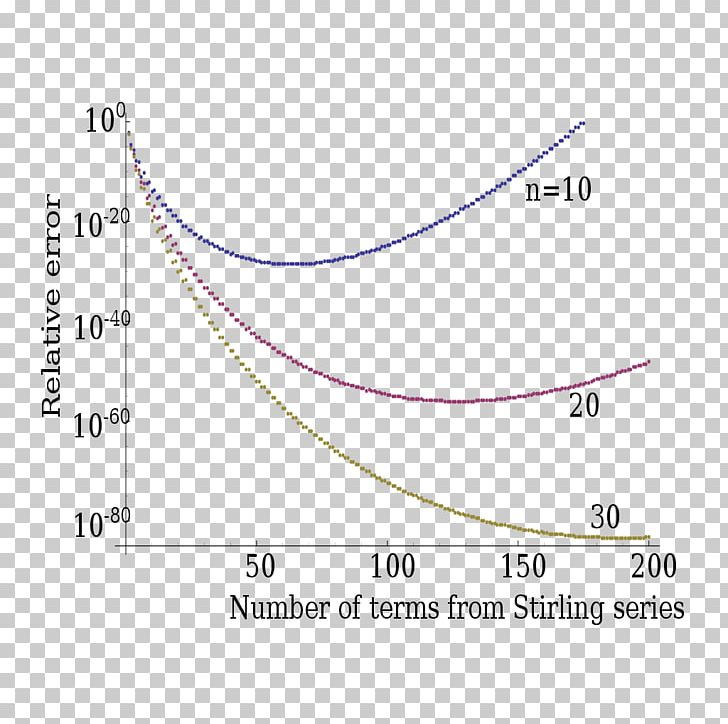
Stirling S Approximation Gamma Function Limit Of A Sequence Angle Area Laplace’s approach to stirling’s formula is noteworthy first, because it makes a direct connection with the gaussian (normal) distribution (whereas in other approaches the gaussian distribution enters indirectly, or not at all), and second, because it provides a general. We could get (15) from laplace’s method by using more terms in the expansion around zero, but this would involve long calculations, and there are much better ways (beyond the scope of this course though). the approximation by a truncated expansion gets more and more accurate as ngrow. but even for n= 5, using only the rst 4 terms we get 5!. The gamma function uniqueness theorem: if a function f(x) satisfies the following three conditions then it is identical to the gamma function. (1) f(x 1) = f(x) (2) the domain of f contains all x>0 and f(x) is log convex (3) f(1)=1. Stirling’s approximation, which states that Γ (n 1) ∼ 2 π n (n e) n as n → ∞, is useful when estimating the order of n!. notably, it is quite accurate even when n is small. the authentic proof entails gamma function and laplace’s method. however in integer case, stirling’s approximation can be approached with poisson distribution. We first remember the definition f the gamma function $ \gamma(n 1) = n! = \int {0}^{\infty} t^{n} e^{ t} dt $ and using this definition we are to prove stirling's approximation formula for very large n $ n! \sim (\frac{n}{e})^n \sqrt{2 \pi n} $. The $\sqrt{2\pi}$ factor in the approximation gives away the special relationship stirling’s approximation has to the gaussian. stirling’s approximation, in combination with laplace’s method used in this article can be used to craft a general methods for proving special cases of the central limit theorem.
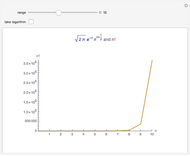
Stirling S Approximation Versus N Wolfram Demonstrations Project The gamma function uniqueness theorem: if a function f(x) satisfies the following three conditions then it is identical to the gamma function. (1) f(x 1) = f(x) (2) the domain of f contains all x>0 and f(x) is log convex (3) f(1)=1. Stirling’s approximation, which states that Γ (n 1) ∼ 2 π n (n e) n as n → ∞, is useful when estimating the order of n!. notably, it is quite accurate even when n is small. the authentic proof entails gamma function and laplace’s method. however in integer case, stirling’s approximation can be approached with poisson distribution. We first remember the definition f the gamma function $ \gamma(n 1) = n! = \int {0}^{\infty} t^{n} e^{ t} dt $ and using this definition we are to prove stirling's approximation formula for very large n $ n! \sim (\frac{n}{e})^n \sqrt{2 \pi n} $. The $\sqrt{2\pi}$ factor in the approximation gives away the special relationship stirling’s approximation has to the gaussian. stirling’s approximation, in combination with laplace’s method used in this article can be used to craft a general methods for proving special cases of the central limit theorem.
