Solved Find The Sum Of All Two Digit Numbers Which When Divided By 4 To solve the problem of finding the sum of all two digit numbers that yield a remainder of 1 when divided by 4, we can follow these steps: 1. identify the form of the numbers: the two digit numbers that leave a remainder of 1 when divided by 4 can be expressed in the form 4k 1, where k is an integer. 2. determine the range of k:. The sum of all two digit numbers which when divided by 4, yield unity as remainder, is. the first two digit number which when divided by 4 leaves remainder 1 is 4⋅ 3 1 = 13 and last is 4⋅24 1 = 97. the sum of all two digit numbers which when divided by 4, yield unity as remainder, is (a) 1100 (b) 1200 (c) 1210 (d) none of these. check answer and.
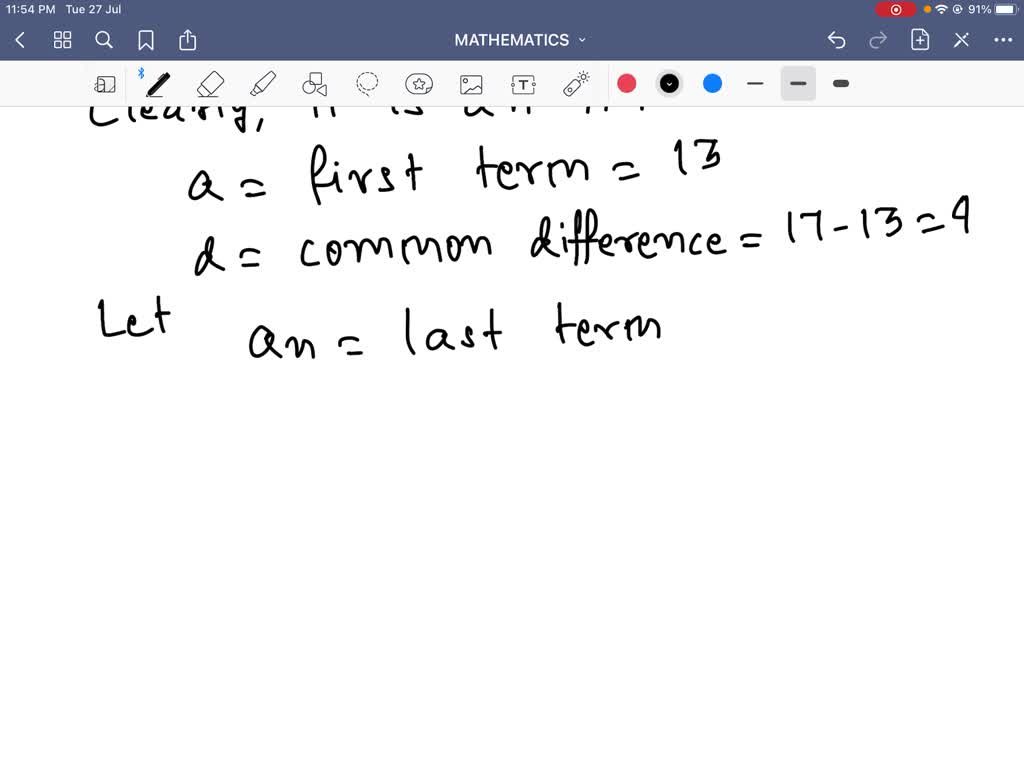
Find The Sum Of All Two Digit Numbers Which When Divided By 4 Yield Find the sum of all two digit numbers which when divided by 4, yields 1 as remainder. Where k is an integer, and n is a two digit number (from 10 to 99). we will find the smallest and largest two digit numbers that satisfy this condition, then sum all such numbers. Detailed solution the first two digit number which when divided by 4 leaves remainder 1 is 4 .3 1 = 13 and last is 4 . 24 1 = 97. thus, we have to find the sum 13 17 21 … 97 which is an a.p. ∴ 97 = 13 (n 1) 4 ⇒ n = 22 and s n = n 2 [a l] = 11 × [13 97] = 11 × 110 = 1210. Sum of all two digit numbers which when divided by 4 yield unity as remainder is.
Find The Sum Of All Two Digit Natural Numbers Which When Divided By 3 Detailed solution the first two digit number which when divided by 4 leaves remainder 1 is 4 .3 1 = 13 and last is 4 . 24 1 = 97. thus, we have to find the sum 13 17 21 … 97 which is an a.p. ∴ 97 = 13 (n 1) 4 ⇒ n = 22 and s n = n 2 [a l] = 11 × [13 97] = 11 × 110 = 1210. Sum of all two digit numbers which when divided by 4 yield unity as remainder is. We need numbers who give remainder as 1 (unity) when divided by 4, so we will add one to all these numbers to get the required series. the new ap is 13, 17, 21, …. Step by step video, text & image solution for find the sum of all two digit numbers which when divided by 4, yields 1 as remainder. by maths experts to help you in doubts & scoring excellent marks in class 11 exams. The first term of an a.p. is a, the second term is b and the last term is c. show that the sum of the a.p. is (𝑏 𝑐 − 2 𝑎) (𝑐 𝑎) 2 (𝑏 − 𝑎). Misc 6 find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.
The Sum Of All Two Digit Positive Numbers Which When Divided By 7 Yield We need numbers who give remainder as 1 (unity) when divided by 4, so we will add one to all these numbers to get the required series. the new ap is 13, 17, 21, …. Step by step video, text & image solution for find the sum of all two digit numbers which when divided by 4, yields 1 as remainder. by maths experts to help you in doubts & scoring excellent marks in class 11 exams. The first term of an a.p. is a, the second term is b and the last term is c. show that the sum of the a.p. is (𝑏 𝑐 − 2 𝑎) (𝑐 𝑎) 2 (𝑏 − 𝑎). Misc 6 find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.
The Sum Of All Two Digit Positive Numbers Which When Divided By 7 Yield The first term of an a.p. is a, the second term is b and the last term is c. show that the sum of the a.p. is (𝑏 𝑐 − 2 𝑎) (𝑐 𝑎) 2 (𝑏 − 𝑎). Misc 6 find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.
The Sum Of All Two Digit Numbers Which When Divided By 4 Yield Unity As
Comments are closed.