
Calculus Iii Surface Integrals Of Vector Fields Pdf Let’s now take a quick look at the formula for the surface integral when the surface is given parametrically by \(\vec r\left( {u,v} \right)\). in this case the surface integral is,. Use a surface integral to calculate the area of a given surface. explain the meaning of an oriented surface, giving an example. describe the surface integral of a vector field. use surface integrals to solve applied problems. we have seen that a line integral is an integral over a path in a plane or in space.

Surface Integrals Vector Calculus Math 243 Instructor Dr Naila In this article, let us discuss the definition of the surface integral, formulas, surface integrals of a scalar field and vector field, examples in detail. in vector calculus, the surface integral is the generalization of multiple integrals to integration over the surfaces. sometimes, the surface integral can be thought of the double integral. In this video we come up formulas for surface integrals, which are when we accumulate the values of a scalar function over a surface. this is analogous to a line integral over a curve. as. Explain the meaning of an oriented surface, giving an example. describe the surface integral of a vector field. use surface integrals to solve applied problems. recall that when we defined a scalar line integral, we did not need to worry about an orientation of the curve of integration. In this section we want to learn how to integrate functions defined on surfaces. this yields a generalisation of double integrals over plane domains to double integrals over curved domains, that is, surfaces.
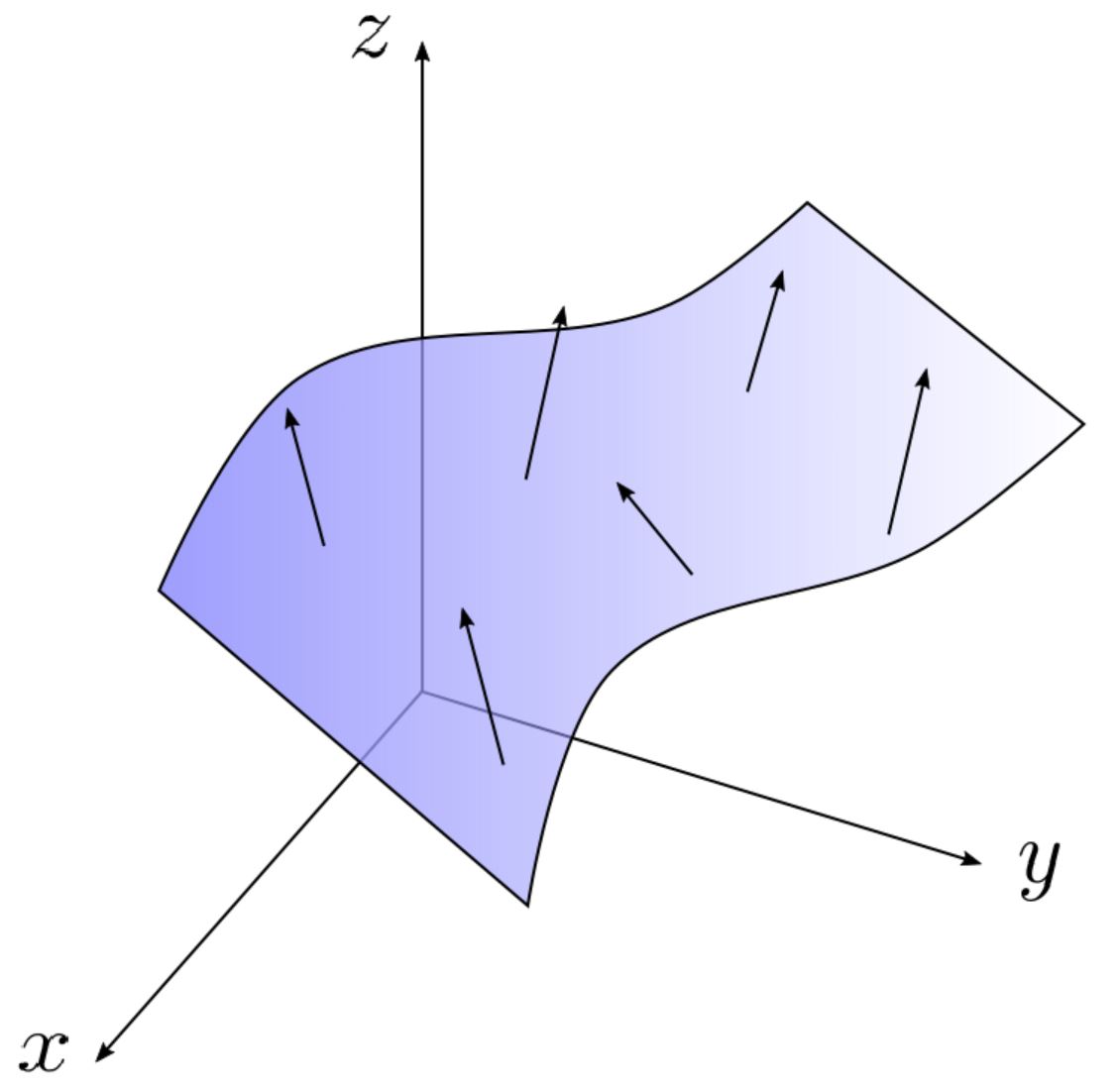
Hartleymath Surface Integrals Explain the meaning of an oriented surface, giving an example. describe the surface integral of a vector field. use surface integrals to solve applied problems. recall that when we defined a scalar line integral, we did not need to worry about an orientation of the curve of integration. In this section we want to learn how to integrate functions defined on surfaces. this yields a generalisation of double integrals over plane domains to double integrals over curved domains, that is, surfaces. The surface integral represents the flux of the vector field through the surface; the choice of projection plane (\(xy\), \(yz\), or \(zx\)) depends on which gives the simplest integral; the unit normal vector \(\hat{n}\) is crucial for correct flux calculation; for closed surfaces, the convention is to take the outward normal. Surface integrals are a natural generalization of line integrals: instead of integrating over a curve, we integrate over a surface in 3 space. such integrals are important in any of the subjects that deal with continuous media (solids, fluids, gases), as well as subjects that deal with force fields, like electromagnetic or gravitational fields. Just as we can integrate functions $f(x,y)$ over regions in the plane, using $$\dint{d} f(x,y)\, da,$$ so we can compute integrals over surfaces in space, using $$\dint{d} f(x,y,z)\, ds.$$ in practice this means that we have a vector function ${\bf r}(u,v)=\langle x(u,v),y(u,v),z(u,v)\rangle$ for the surface, and the integral we compute is. Normal vectors ~n1 and ~n2 = ~n1 at (x; y; z). if it is possible to chose a unit normal vector ~n at every such point (x; y; z) so that ~n varies continuously over s, then s is called an oriented surface and the gi. en choice of ~n provides s with an orientation. there are two p.

Surface Integrals Of Vector Fields Mh2100 Calculus Iii Ntu The surface integral represents the flux of the vector field through the surface; the choice of projection plane (\(xy\), \(yz\), or \(zx\)) depends on which gives the simplest integral; the unit normal vector \(\hat{n}\) is crucial for correct flux calculation; for closed surfaces, the convention is to take the outward normal. Surface integrals are a natural generalization of line integrals: instead of integrating over a curve, we integrate over a surface in 3 space. such integrals are important in any of the subjects that deal with continuous media (solids, fluids, gases), as well as subjects that deal with force fields, like electromagnetic or gravitational fields. Just as we can integrate functions $f(x,y)$ over regions in the plane, using $$\dint{d} f(x,y)\, da,$$ so we can compute integrals over surfaces in space, using $$\dint{d} f(x,y,z)\, ds.$$ in practice this means that we have a vector function ${\bf r}(u,v)=\langle x(u,v),y(u,v),z(u,v)\rangle$ for the surface, and the integral we compute is. Normal vectors ~n1 and ~n2 = ~n1 at (x; y; z). if it is possible to chose a unit normal vector ~n at every such point (x; y; z) so that ~n varies continuously over s, then s is called an oriented surface and the gi. en choice of ~n provides s with an orientation. there are two p.
