
Sut Pdf On studocu you find all the lecture notes, summaries and study guides you need to pass your exams with better grades. Thus, instructions i7, i8, and i9 can be issued without stalling on i5 and we can issue a loop every 9 cycles (and complete the previous iteration of the loop every nine cycles). a fully pipelined multiplier is necessary to allow a new multiply instruction to be issued every 9 cycles.

Sut2019 Xlsx Sut I1 I2 I3 I4 I5 I6 I7 I8 I9 I10 I11 I12 I13 I14 I15 Intel targets many customer sectors with its core processors. there is a clear hierarchy expressed by the name convention: i3: entry level (basic task like office work and web browsing). i5:. Compute: i1 , i2, i3, i4, i5, i6, i7, i8, i9, i10, i11, ib, ir, iw please show work! your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. I1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i i11 i12 i13 i14 i15 i16 i17 i18 i19 i20 i1 i2 i3 i4 i5 i6 i7 i8 i i9 i10 i11 i12 i13 i14 i15 i16 i i17 i18 i19 i20 i21 i22 i23 i24 h1 h2 h3 h4 h5 h6 h7 h8 h h9 h10 h11 h12 h13 h14 h15 h16 h h17 h18 h19 h20 h21 h22 h23 h24. For instance, i2 i4 on r2. also i1 i3=i7=i11(r1), i2 i4=i6=i8=i10(r2), i3 i7=i11(r1), i4 i6=i8=i10(r2), i5 i9(r3), i6 i8=i10(r2), i7 i11(r1), i8 i10(r2). read{write (false or fake) dependency: all the pairs of occurrences of a register ri where instruction ij reads from ri and instruction ik writes to ri with j < k. for instance, i3 i4 on r2.

Unit 4 Xlsx Activity Id P1 P2 P3 P4 S1 S2 D1 D2 D3 D4 I1 I2 I3 I4 V1 I1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i i11 i12 i13 i14 i15 i16 i17 i18 i19 i20 i1 i2 i3 i4 i5 i6 i7 i8 i i9 i10 i11 i12 i13 i14 i15 i16 i i17 i18 i19 i20 i21 i22 i23 i24 h1 h2 h3 h4 h5 h6 h7 h8 h h9 h10 h11 h12 h13 h14 h15 h16 h h17 h18 h19 h20 h21 h22 h23 h24. For instance, i2 i4 on r2. also i1 i3=i7=i11(r1), i2 i4=i6=i8=i10(r2), i3 i7=i11(r1), i4 i6=i8=i10(r2), i5 i9(r3), i6 i8=i10(r2), i7 i11(r1), i8 i10(r2). read{write (false or fake) dependency: all the pairs of occurrences of a register ri where instruction ij reads from ri and instruction ik writes to ri with j < k. for instance, i3 i4 on r2. Given: i9 i10 i11 i12 . to find: express the given equation in a ib we know that, i0=1, i6= 1. i1=i, i7= i. i2= 1, i8=1. i3= i, i9=i. i4=1, i10= 1. i5=i, i11= i =(i3)3 (i5)2 ( 1) ( i) (1) =( i) 2i 1 i 1 = 2i 2i 1 1 =0i 0. so, the correct answer after solving is 0i 0 which is in the form of a ib. Answer to calculate i1, i2, i3, i4, i5, i6, i7, i8, and. Find the multiplicative inverse of the complex number. –i. if x – i y = prove that ( ) = . if (a ib) (c id) (e if) (g ih) = a ib, then show that (a 2 b 2) (c 2 d 2) (e 2 f 2) (g 2 h 2) = a 2 b 2. if (1 i 1 i) m = 1, then find the least positive integral value of m. find the value of i i 2 i 3 i 4. I1 i2 i3 i4 i5 i6 x x i7 i8 i9 i10 i11 i15 j14 j16 m4 m5 j1 j2 j3 j4 j5 i13 l1 k1 k2 k3 k4 k5 l2 l3 l4 l5 l6 f5 f6 f7 m2 m3 l7 l8 l9 l10 i6 i7 i8 i9 j6 j7 j8 j9 i5 g9 g10 g11 i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13 i14 i15 i16 h1 h2 h3 h4 h5 h6 h7 h8 h9 h10 h11 h12 h13 h14 h15 h16.
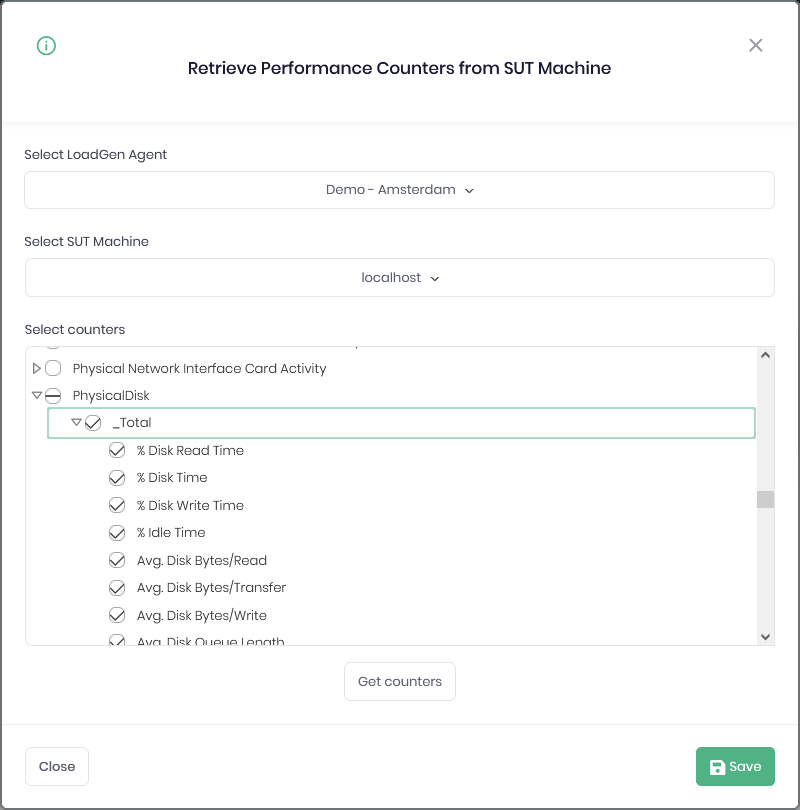
Systems Under Test Sut Sut Templates Loadgen Given: i9 i10 i11 i12 . to find: express the given equation in a ib we know that, i0=1, i6= 1. i1=i, i7= i. i2= 1, i8=1. i3= i, i9=i. i4=1, i10= 1. i5=i, i11= i =(i3)3 (i5)2 ( 1) ( i) (1) =( i) 2i 1 i 1 = 2i 2i 1 1 =0i 0. so, the correct answer after solving is 0i 0 which is in the form of a ib. Answer to calculate i1, i2, i3, i4, i5, i6, i7, i8, and. Find the multiplicative inverse of the complex number. –i. if x – i y = prove that ( ) = . if (a ib) (c id) (e if) (g ih) = a ib, then show that (a 2 b 2) (c 2 d 2) (e 2 f 2) (g 2 h 2) = a 2 b 2. if (1 i 1 i) m = 1, then find the least positive integral value of m. find the value of i i 2 i 3 i 4. I1 i2 i3 i4 i5 i6 x x i7 i8 i9 i10 i11 i15 j14 j16 m4 m5 j1 j2 j3 j4 j5 i13 l1 k1 k2 k3 k4 k5 l2 l3 l4 l5 l6 f5 f6 f7 m2 m3 l7 l8 l9 l10 i6 i7 i8 i9 j6 j7 j8 j9 i5 g9 g10 g11 i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13 i14 i15 i16 h1 h2 h3 h4 h5 h6 h7 h8 h9 h10 h11 h12 h13 h14 h15 h16.
Systems Under Test Sut Sut Templates Loadgen Find the multiplicative inverse of the complex number. –i. if x – i y = prove that ( ) = . if (a ib) (c id) (e if) (g ih) = a ib, then show that (a 2 b 2) (c 2 d 2) (e 2 f 2) (g 2 h 2) = a 2 b 2. if (1 i 1 i) m = 1, then find the least positive integral value of m. find the value of i i 2 i 3 i 4. I1 i2 i3 i4 i5 i6 x x i7 i8 i9 i10 i11 i15 j14 j16 m4 m5 j1 j2 j3 j4 j5 i13 l1 k1 k2 k3 k4 k5 l2 l3 l4 l5 l6 f5 f6 f7 m2 m3 l7 l8 l9 l10 i6 i7 i8 i9 j6 j7 j8 j9 i5 g9 g10 g11 i1 i2 i3 i4 i5 i6 i7 i8 i9 i10 i11 i12 i13 i14 i15 i16 h1 h2 h3 h4 h5 h6 h7 h8 h9 h10 h11 h12 h13 h14 h15 h16.

Sut 5 Summary Of Sut 4 1 Inf 171 Studocu
