Symmetric Groups Abstract Algebra

Abstract Algebra Pdf Group Mathematics Group Theory In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. in particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. [1] . \(s n\) with compositions forms a group; this group is called a symmetric group. \(s n\) is a finite group of order \(n!\) and are permutation groups consisting of all possible permutations of n objects. identity permutation is denoted as \(e\). we will denote a permutation by \(\sigma = \begin{bmatrix} 1 & 2& 3& \cdots & n\\.

Group Abstract Algebra Ppt We will study permutations, and how to write them concisely in cycle notation. cayley's theorem tells us that every nite group is isomorphic to a collection of permutations (i.e., a subgroup of a symmetric group). a permutation is an action that rearranges a collection of objects. There are two concepts which are very similar literally in abstract algebra: symmetric group and symmetry group. by definition, the symmetric group on a set is the group consisting of all bijections of the set (all one to one and onto functions) from the set to itself with function composition as the group operation. General linear group gl(n;f), as well as certain other linear groups. the purpose of this chapter is to derive some of the elementary proper ties of s(n). for example, we will see that there are several standard ways of representing its elements. we will also take a somewhat historical sidetrip. Sasha patotski (cornell university) symmetric groups. abstract groups. november 9, 2015 6 10. sign of a permutation de nition for ˙2s n de ne inv(˙) to be the number of pairs (ij) such that i ˙(j). this number inv(˙) is called the number of inversions of ˙.

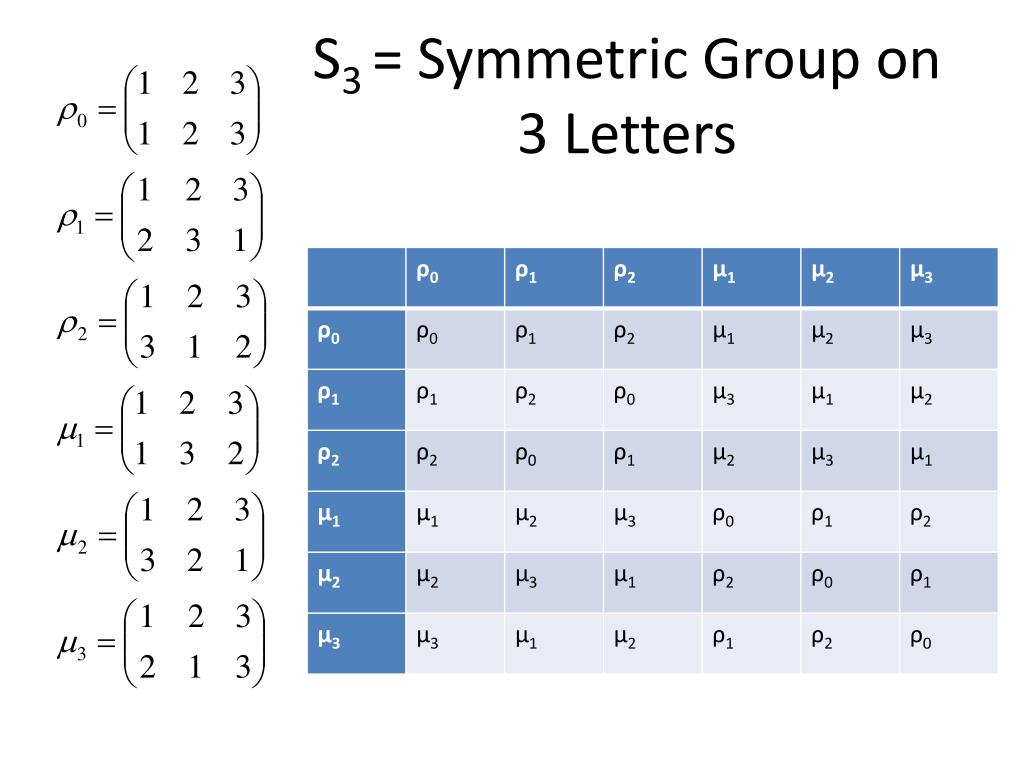
Ppt Math 3121 Abstract Algebra I Powerpoint Presentation Free General linear group gl(n;f), as well as certain other linear groups. the purpose of this chapter is to derive some of the elementary proper ties of s(n). for example, we will see that there are several standard ways of representing its elements. we will also take a somewhat historical sidetrip. Sasha patotski (cornell university) symmetric groups. abstract groups. november 9, 2015 6 10. sign of a permutation de nition for ˙2s n de ne inv(˙) to be the number of pairs (ij) such that i ˙(j). this number inv(˙) is called the number of inversions of ˙. N "same shape". in abstract algebra, momorphism is a special correspondence between elemens. of two groups. whereas isomorphism is a function that captures a one to one relationship between two iso. orphism groups. if there exists an between two groups, then the groups are isomorphic homom. rphism called . an isomorphism is a s. ich i. f real nu. So why not a multi volume series in abstract algebra for those who are have less experience but are nevertheless interested in undertaking a serious course in abstract algebra? this is the first volume in the series. it is devoted to group theory. subsequent volumes will be devoted to rings, fields, vector spaces and modules. 5 symmetric groups and dihedral groups 5.1 symmetric groups recall that, given an integer n ≥2, the n th symmetric group s n is the set of bijective maps from the set i n = {1, ,n}onto itself equipped with the composition of maps. elements of s n are called permutations (of i n). for example, an element in s 10 is of the form 1 2 3 4 5 6 7. Let x be a set. then the symmetric group on x is the group of all bijections. with functional composition as operation. it is denoted by sx . are each other's inverses; thus, they are bijections. furthermore, these assignments respect the group operations of sx and sy, showing these two groups to be isomorphic.