Solved 4c1 B1 C1 Of 10 36 B2 C2 Is 7 Then The Determinant Chegg The determinant is a number associated with any square matrix; we’ll write it as det a or |a|. the determinant encodes a lot of information about the matrix; the matrix is invertible exactly when the determinant is non zero. M in terms of the columns of a: det a = det(a1, a2, . . . , an). it is often helpful to think of the determ nant as the volume of the parallelepiped spanned by the columns. from this view, since the volume is the standard unit cube.
Using Properties Of Determinants Show The Following B C 2 Ab Ca The determinant |a2 a2 (b c)2 b c b2 b2 (c a)2 c a c2 c2 (a b)2 a b| is divisible by: (a) a b c (b) (a b) (b c) (c a) (c) a2 b2 c2 (d) (a b) (b c) (c a). Using properties of determinants, prove the following: | (a 2,a 2 (b c) 2, bc) (b 2,b 2 (c a) 2,ca) (c 2,c 2 (a b) 2,ab)| = (a b) (b c) (c a) (a b c) (a 2 b 2 c 2). The correct answer is using c2→c2−c1−2c3, then c1→c1 c2 take a2 b2 c2 common from first column]. Determinant formulas and cofactors now that we know the properties of the determinant, it’s time to learn some (rather messy) formulas for computing it.
Question 11 Show That Determinant Abc 1 1 A 1 B 1 C Abc The correct answer is using c2→c2−c1−2c3, then c1→c1 c2 take a2 b2 c2 common from first column]. Determinant formulas and cofactors now that we know the properties of the determinant, it’s time to learn some (rather messy) formulas for computing it. There are two $b^2$ terms: $ab^2 cb^2$. this can be factored into $b^2 (a c)= b^2 (c a)$. there are two $b$ terms: $abc c^2b$. To find the value of the determinant of the given matrix, we can use the formula for the determinant of a 3x3 matrix. the determinant of a matrix a =⎝⎛a d g b e h c f i⎠⎞ is given by det(a) =a(ei−f h)−b(di−f g) c(dh−eg). we will apply this formula to the given matrix. The divisors of the determinant d = ∣∣ ca2 b2 a b c ab2 c2 b c a bc2 a2 ∣∣ is (a,b,c ∈ r). We need to find its determinant and show that it simplifies to (a b c)(a2 b2 c2). we will calculate the determinant using the standard expansion method (cofactor expansion along the first row).
Question 11 Show That Determinant Abc 1 1 A 1 B 1 C Abc There are two $b^2$ terms: $ab^2 cb^2$. this can be factored into $b^2 (a c)= b^2 (c a)$. there are two $b$ terms: $abc c^2b$. To find the value of the determinant of the given matrix, we can use the formula for the determinant of a 3x3 matrix. the determinant of a matrix a =⎝⎛a d g b e h c f i⎠⎞ is given by det(a) =a(ei−f h)−b(di−f g) c(dh−eg). we will apply this formula to the given matrix. The divisors of the determinant d = ∣∣ ca2 b2 a b c ab2 c2 b c a bc2 a2 ∣∣ is (a,b,c ∈ r). We need to find its determinant and show that it simplifies to (a b c)(a2 b2 c2). we will calculate the determinant using the standard expansion method (cofactor expansion along the first row).
Solved Knowing A1 A2 A3 C1 C2 C3 Find The Determinant Of The Chegg The divisors of the determinant d = ∣∣ ca2 b2 a b c ab2 c2 b c a bc2 a2 ∣∣ is (a,b,c ∈ r). We need to find its determinant and show that it simplifies to (a b c)(a2 b2 c2). we will calculate the determinant using the standard expansion method (cofactor expansion along the first row).
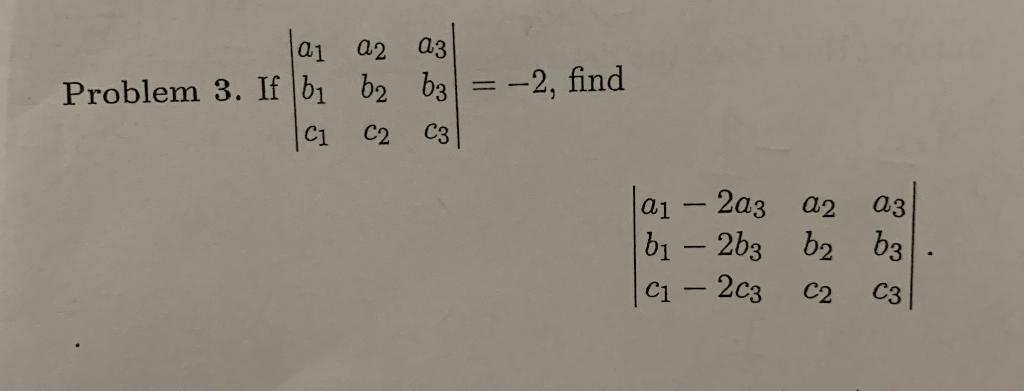
Solved If A Determinant Of A Matrix A1 A 2 A3 B1 B2 B3 Chegg
Comments are closed.