
Unit 1 Part Ii Pdf Group Mathematics Ring Mathematics In this video we discuss the multiplicative group of units of a ring. Let r be a ring and g a group. the group ring rg is the free r module with basis g, i.e. it consists of all formal sums. ! ! g j rg 6= 0g. x aug : rg ! r : rgg 7!x rg: x aug g;n;rrg ! r(g=n) : rgg 7!x rg(gn): g2g. the kernel of augg;n;r is the augmentation ideal of rg modulo n.

Pdf Units Of The Group Ring The unit group of the ring m n (r) of n × n matrices over a ring r is the group gl n (r) of invertible matrices. for a commutative ring r , an element a of m n ( r ) is invertible if and only if the determinant of a is invertible in r . Let $\mathbb{q}$ be the rationals and $g$ a group. then we consider the group ring $\mathbb{q}[g]$. since the operation on $\mathbb{q}[g]$ restricted to $g$ is just the group operation, i know that $g$ is a subgroup of the units of $\mathbb{q}[g]$. how can we describe all units of $\mathbb{q}[g]$?. Definition 1.1. a representation of a group g over a field k is defined to be a group homomorphism ρ: g → aut k(v) where v is a vector space over k. here aut k(v) is the group of k linear automorphisms of v. this also written as gl k(v). this is the group of units of the ring end k(v)= hom k(v,v) which, as i explained before, is a ring. Form a group called the group of units u(r). proposition 2.2. u is a functor from the category of rings to the category of groups. proof. any ring homomorphism ˚: r!stakes units to units since xy= yx= 1 implies ˚(xy) = ˚(x)˚(y) = ˚(yx) = ˚(y)˚(x) = ˚(1) = 1: in the next example, i constructed the adjoint of this functor. 2.3. group.
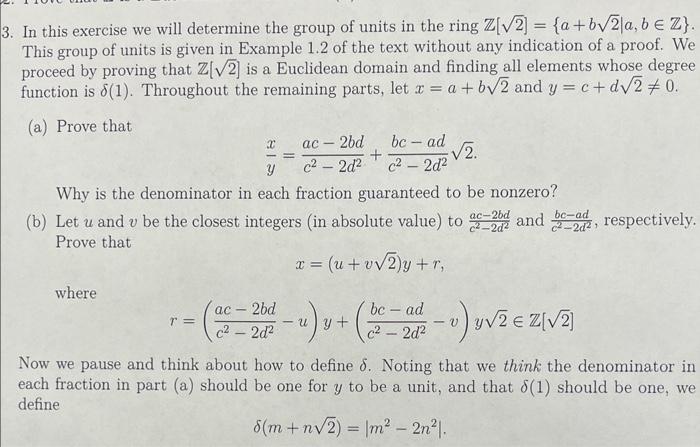
Solved In This Exercise We Will Determine The Group Of Units Chegg Definition 1.1. a representation of a group g over a field k is defined to be a group homomorphism ρ: g → aut k(v) where v is a vector space over k. here aut k(v) is the group of k linear automorphisms of v. this also written as gl k(v). this is the group of units of the ring end k(v)= hom k(v,v) which, as i explained before, is a ring. Form a group called the group of units u(r). proposition 2.2. u is a functor from the category of rings to the category of groups. proof. any ring homomorphism ˚: r!stakes units to units since xy= yx= 1 implies ˚(xy) = ˚(x)˚(y) = ˚(yx) = ˚(y)˚(x) = ˚(1) = 1: in the next example, i constructed the adjoint of this functor. 2.3. group. In this section we determine the structure of the unit group of r{g, c), wher ge is a finite abelian group, and c is the integer ring of a finite algebraic extension k' of the rational field k. Definition: unit in a ring. an element x ∈ r is said to be a unit if xy = yx=1forsomey ∈ r. the set of units of a ring r is denoted by r×. note that in contrast with the zero divisor concept, the element 1 is counted as a unit. it is easily seen the the set r× is a group under multiplication. 9. definition: divisibility in a ring. we. Definition 1.3 (group of units). the group of units u(r) of a ring (r, , ) are the group of units of the monoid (r, ) i.e., u(r) = {u ∈ r|∃v ∈ r such that uv = 1 = vu}. notice that in a ring (r, , ), only distributivity relates the two oper ations. In a commutative ring, a ring product is a unit iff all are units. the group e of the units of the ring r is called the group of units of the ring . if r is a field, e is said to be the multiplicative group of the field .
