Cho Gгіc Xoy Trгєn Tia Ox Lбєґy Hai д Iб ѓm A M Trгєn Tia Oy Lбєґy Hai д Iб ѓm B Bài 1 cho ot là tia phân giác của góc nhọn xoy. trên tia ox lấy điểm a, trên tia oy lấy điểm b sao cho oa=ob. trên tia ot lấy diểm m sao cho om>oa. bài 1: cho tam giác abc cân (abac), o là giao điểm 3 trung trực 2 cạnh của tam giác abc (o nằm trong tam giác). trên tia đối của các tia ab và ca ta lấy 2 điểm m, n sao cho amcn. Bài 7. cho góc xoy nhọn. lấy điểm a trên tia ox, điểm b trên tia oy. trên tia ox lấy điểm c sao cho bc là tia phân giác của góc aby. gọi i là giao điểm của hai tia phân giác góc xab và xoy. chứng minh ba điểm b, i, c thẳng hàng.

Bг I 7 Cho Gгіc Xoy Nhб ќn Lбєґy д Iб ѓm A Trгєn Tia Ox д Iб ѓm B Trгєn Tia Oy Bài 28 trang 75 sách bài tập toán lớp 7 tập 2: cho góc xoy. trên tia ox lấy điểm c, trên tia oy lấy điểm d sao cho oc = od. vẽ một phần đường tròn tâm c và tâm d có cùng bán kính, e là điểm chung của hai phần đường tròn đó (e nằm trong góc xoy) ( hình 15 ). Cho góc xoy là góc nhọn, trên tia oy lấy điểm b, trên tia ox lấy điểm a sao cho ob=oa. vẽ tia ot là tia phân giác của góc xoy cắt đoạn thẳng ba tại h. lấy điểm c bất kì thuộc tia ot. chứng minh: ot vuông góc ab. Cho góc nhọn xoy, trên tia ox lấy điểm a, trên tia oy lấy điểm b sao cho oa = ob. gọi h là trung điểm của đoạn thẳng ab. a) chứng minh: \(\delta oah = \delta obh\). b) từ a vẽ đường thẳng vuông góc với oa, cắt tia oh tại c. chứng minh: \(cb. Bài 2. mĐ1 cho góc nhọn xoy có om là tia phân giác, ceom(c o) . trên tia ox lấy điểm trên tia oy lấy điểm b sao cho o4=ob . chứng minh: c4=cb. bài 3, mĐ1 cho a4bc = amnp gọi o và g lần lượt là trung điểm của các cạnh bc và np chứng minh.
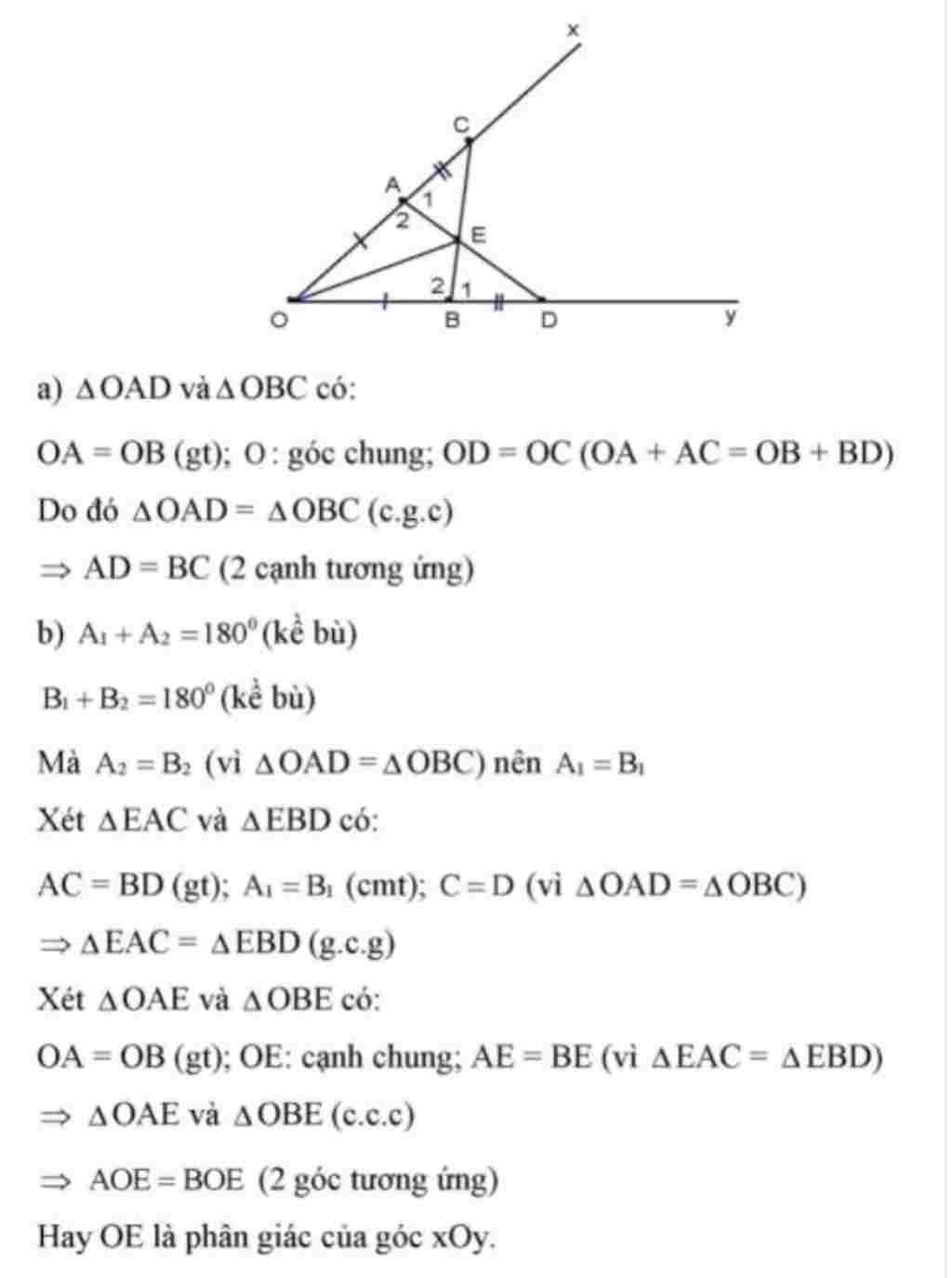
Toгўn Lб P 7 Cho Gгіc Nhб ќn Xoy Trгєn Tia Ox Lбєґy д Iб ѓm A Trгєn Tia Oy Lбєґy Cho góc nhọn xoy, trên tia ox lấy điểm a, trên tia oy lấy điểm b sao cho oa = ob. gọi h là trung điểm của đoạn thẳng ab. a) chứng minh: \(\delta oah = \delta obh\). b) từ a vẽ đường thẳng vuông góc với oa, cắt tia oh tại c. chứng minh: \(cb. Bài 2. mĐ1 cho góc nhọn xoy có om là tia phân giác, ceom(c o) . trên tia ox lấy điểm trên tia oy lấy điểm b sao cho o4=ob . chứng minh: c4=cb. bài 3, mĐ1 cho a4bc = amnp gọi o và g lần lượt là trung điểm của các cạnh bc và np chứng minh. Cho góc nhọn x o y ^, trên tia ox lấy điểm a; trên tia oy lấy b sao cho oa = ob. Đường trung trực của oa và đường trung trực của ob cắt nhau tại i. khi đó: a. oi là tia phân giác x o y ^. Bài 34 trang 71 sgk toán lớp 7 tập 2: cho góc xoy khác góc bẹt. trên tia ox lấy hai điểm a và b, trên tia oy lấy hai điểm c và d sao cho oa = oc, ob = od. gọi i là giao điểm của hai đoạn thẳng ad và bc. Trên tia ox lấy hai điểm a, c (a nằm giữa o và c), trên tia oy lấy hai điểm b, d ( b nằm giữa o và d ) sao cho oa=ob; ac=bd. b) gọi e là giao điểm của ad và bc. chứng minh tam giác eac bằng tam giác ebd. a) ta có oa=ob và ac=bd. vì oa=ob nên tam giác oab là tam giác cân. do đó, ta có ∠oab=∠oba. tương tự, ta có ∠acb=∠cbd. Cho góc nhọn xoy, lấy điểm a trên tia ox (điểm a khác o) và điểm b trên tia oy sao cho oa = ob. gọi m là trung điểm của ab.a) chứng minh: \(\angle oam = \angle obm\)b) trên tia om lấy điểm h sao cho om < oh.

Main 2 D0 Bc D0 Be D1 80 D0 Be D0 B7 D0 B0 Illustrators Cho góc nhọn x o y ^, trên tia ox lấy điểm a; trên tia oy lấy b sao cho oa = ob. Đường trung trực của oa và đường trung trực của ob cắt nhau tại i. khi đó: a. oi là tia phân giác x o y ^. Bài 34 trang 71 sgk toán lớp 7 tập 2: cho góc xoy khác góc bẹt. trên tia ox lấy hai điểm a và b, trên tia oy lấy hai điểm c và d sao cho oa = oc, ob = od. gọi i là giao điểm của hai đoạn thẳng ad và bc. Trên tia ox lấy hai điểm a, c (a nằm giữa o và c), trên tia oy lấy hai điểm b, d ( b nằm giữa o và d ) sao cho oa=ob; ac=bd. b) gọi e là giao điểm của ad và bc. chứng minh tam giác eac bằng tam giác ebd. a) ta có oa=ob và ac=bd. vì oa=ob nên tam giác oab là tam giác cân. do đó, ta có ∠oab=∠oba. tương tự, ta có ∠acb=∠cbd. Cho góc nhọn xoy, lấy điểm a trên tia ox (điểm a khác o) và điểm b trên tia oy sao cho oa = ob. gọi m là trung điểm của ab.a) chứng minh: \(\angle oam = \angle obm\)b) trên tia om lấy điểm h sao cho om < oh.

Cã U 1 Cho Tam Giã C Abc Gã C B Gã C C Tia Phã N Giã C Cá A Gã C Cá A Gã C B Trên tia ox lấy hai điểm a, c (a nằm giữa o và c), trên tia oy lấy hai điểm b, d ( b nằm giữa o và d ) sao cho oa=ob; ac=bd. b) gọi e là giao điểm của ad và bc. chứng minh tam giác eac bằng tam giác ebd. a) ta có oa=ob và ac=bd. vì oa=ob nên tam giác oab là tam giác cân. do đó, ta có ∠oab=∠oba. tương tự, ta có ∠acb=∠cbd. Cho góc nhọn xoy, lấy điểm a trên tia ox (điểm a khác o) và điểm b trên tia oy sao cho oa = ob. gọi m là trung điểm của ab.a) chứng minh: \(\angle oam = \angle obm\)b) trên tia om lấy điểm h sao cho om < oh.
