Truth Tables And Equivalent Statements Brokeasshome

Truth Tables Tautologies Logicall Equivalent Statements Pdf If And When two statements always have the same truth values, we say that the statements are logically equivalent. to show that equivalence exists between two statements, we use the biconditional if and only if. In both the previous section and also the introduction to this section, we’ve utilized truth tables to analyse the conditions under which our compound logical statements are true or false. we’ve used this structures without much explanation though, so we’ll take a moment to discuss them here.

Truth Tables And Equivalent Statements In this section, you will learn how to determine whether two statements are logically equivalent using truth tables, and then you will apply this knowledge to compose logically equivalent forms of the conditional statement. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. upvoting indicates when questions and answers are useful. what's reputation and how do i get it? instead, you can save this post to reference later. So, if we want to determine prove whether or not statements such as p=(¬p∨¬q) and q=¬(p∧q) are logically equivalent, all we need to do is build a truth table that breaks down both p and q and see if the columns for ¬p∨¬q and ¬(p∧q) are the same in all their truth values. Because complex boolean statements can get tricky to think about, we can create a truth table to break the complex statement into simple statements, and determine whether they are true or false.

Truth Tables And Equivalent Statements Brokeasshome So, if we want to determine prove whether or not statements such as p=(¬p∨¬q) and q=¬(p∧q) are logically equivalent, all we need to do is build a truth table that breaks down both p and q and see if the columns for ¬p∨¬q and ¬(p∧q) are the same in all their truth values. Because complex boolean statements can get tricky to think about, we can create a truth table to break the complex statement into simple statements, and determine whether they are true or false. When you're constructing a truth table, you have to consider all possible assignments of true (t) and false (f) to the component statements. for example, suppose the component statements are p, q, and r. each of these statements can be either true or false, so there are possibilities. Truth table for the compound statement: r (p^ q) theorem a logical statement having n com. onents wil. rgan's laws example 2 show that p ( p): example . Two statement forms are logically equivalent if and only if they have identical truth values for each possible subsitution of statements for their statement variables. the logical equivalence of statement forms p and q is denoted by: p == q (equals with 3 lines) for the truth values of q.
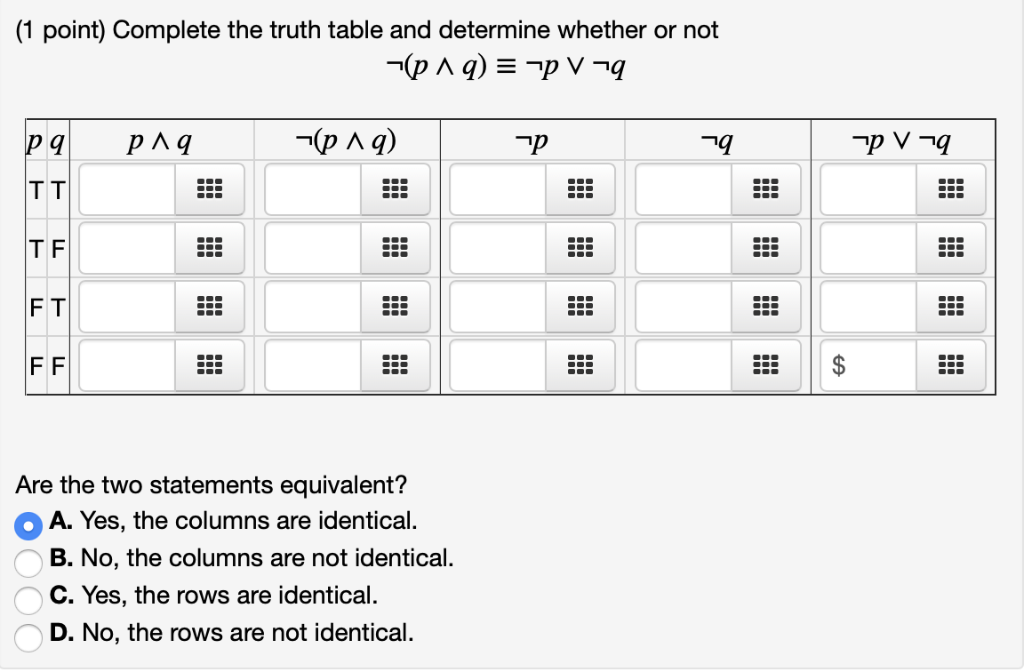
Truth Tables And Equivalent Statements Brokeasshome When you're constructing a truth table, you have to consider all possible assignments of true (t) and false (f) to the component statements. for example, suppose the component statements are p, q, and r. each of these statements can be either true or false, so there are possibilities. Truth table for the compound statement: r (p^ q) theorem a logical statement having n com. onents wil. rgan's laws example 2 show that p ( p): example . Two statement forms are logically equivalent if and only if they have identical truth values for each possible subsitution of statements for their statement variables. the logical equivalence of statement forms p and q is denoted by: p == q (equals with 3 lines) for the truth values of q.
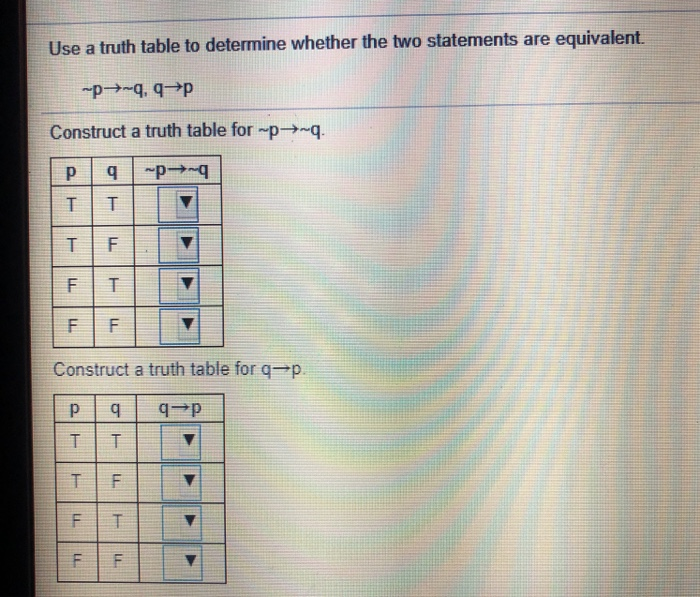
Truth Tables And Equivalent Statements Brokeasshome Two statement forms are logically equivalent if and only if they have identical truth values for each possible subsitution of statements for their statement variables. the logical equivalence of statement forms p and q is denoted by: p == q (equals with 3 lines) for the truth values of q.
Comments are closed.