Use The Reduction Of Order Formula To Find Another Solution To Y 16y 0 Given Y_1 Cos4x

Solved 1 Use The Reduction Of Order Formula To Find A Chegg Use the reduction of order formula to find another solution to y'' 16y = 0 given y 1 = cos (4x). Use reduction of order (or the formula) to find a second solution: $y'' 16y=0$ given $y 1=cos4x$ the formula they refer to is $y 2=\int\frac {e^ { \int p (x)dx}} {y 1^2}dx$ so $y 2=cos4x \int \frac {e.

Solved 2 Use Reduction Of Order Formula Find The General Chegg To solve the differential equation y′′ 16y = 0 using the reduction of order method, given that y1 = cos(4x) is a known solution, we start by looking for a second solution of the form y2 = u(x)y1, where u(x) is an unknown function. The method of reduction of order is a technique for finding a second solution to a second order linear differential equation when one solution is already known. This is known as reduction of order, because it reduces the problem of finding a solution of a second order equation to that of solving a related first order equation. The “reduction of order method” is a method for converting any linear differential equation to another linear differential equation of lower order, and then constructing the general solution to the original differential equation using the general solution to the lower order equation.

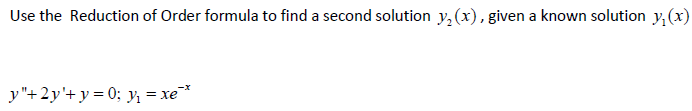
Solved Use The Reduction Of Order Formula To Find A Second Chegg This is known as reduction of order, because it reduces the problem of finding a solution of a second order equation to that of solving a related first order equation. The “reduction of order method” is a method for converting any linear differential equation to another linear differential equation of lower order, and then constructing the general solution to the original differential equation using the general solution to the lower order equation. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. To solve the differential equation y′′ 16y =0 using reduction of order, we start with the known solution y1 = cos(4x). we will use the formula for reduction of order: y= y1(x)∫ (y1(x))2e−∫ p(x)dx dx where p(x) is the coefficient of y in the original equation. Given a differential equation with one solution, use reduction of order to find a second solution. the equation is transformed into standard form for ease of calculation. Manually deriving the second solution using reduction of order involves multiple integral steps. this calculator generates the integral formula instantly, helping you focus on the integral evaluation.