Solved Exercise 1 Orthogonal Projections 3 3 3 4 6 3 Chegg How to find vector projections & orthogonal components (calculus 3 lesson 10) ️ download my free vector cheat sheets: jkmathematics vector ch. Projections and components: the geometric definition of dot product helps us express the projection of one vector onto another as well as the component of one vector in the direction of another.
Solved 1 Point Let A 3 6 6 And B 10 5 1 Be Chegg A nonzero vector ~a is de ned to be orthogonal or perpendicular or normal to a nonzero vector ~b, if the angle from ~a to ~b is equal to the angle from ~b to ~a. why use the dot product? if the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as ~a. Learn about vectors, their operations, and their applications in two dimensional and three dimensional space. learn about multivariable functions and apply calculus to them, including partial derivatives and multiple integration. In this problem, we delve into the concepts of vector projection and orthogonality within the framework of three dimensional vectors. Inverse trigonometric functions and basic trigonometric equations1h 41m. © 1996– 2025 pearson all rights reserved.
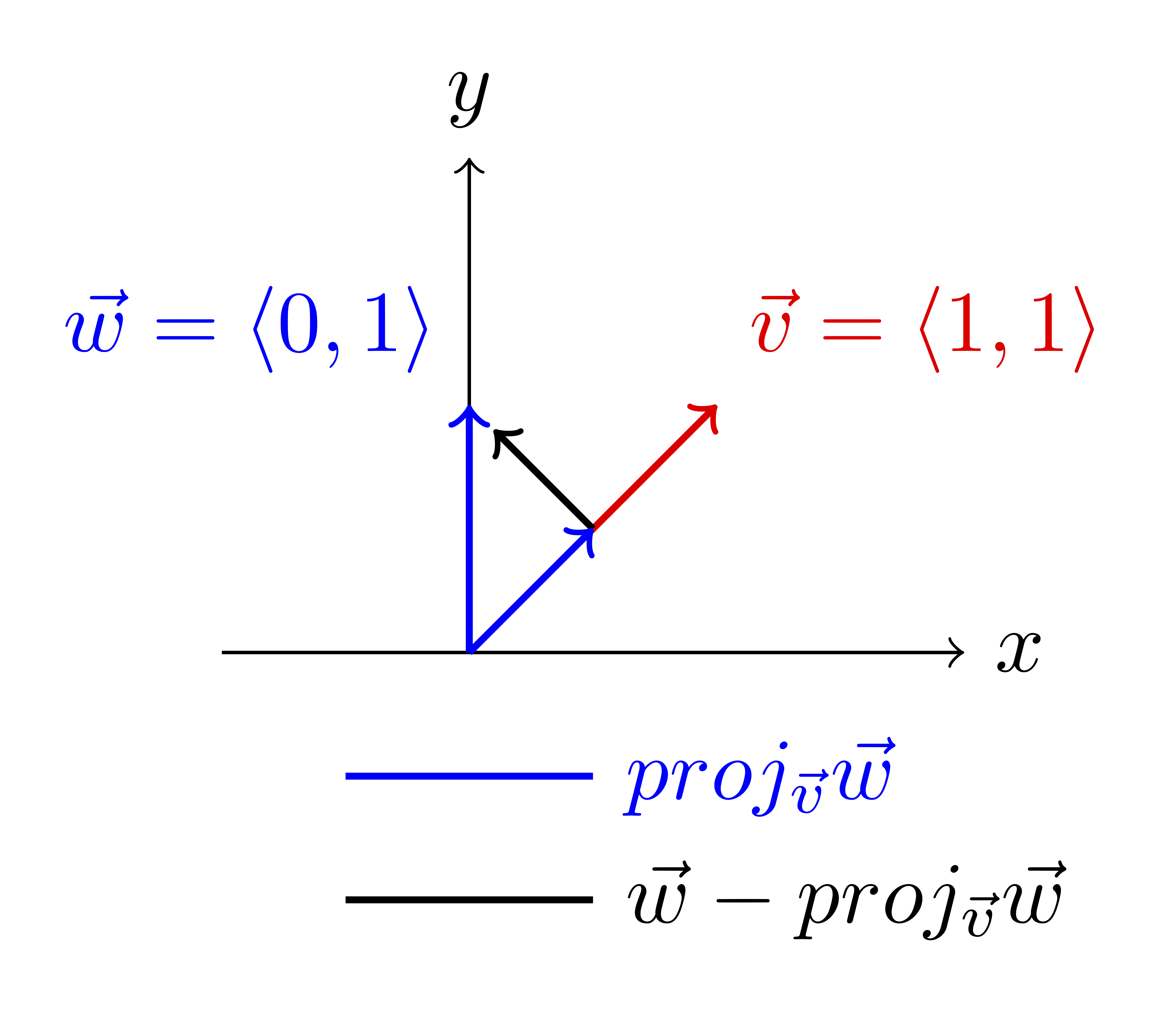
Orthogonal Projections Vrogue Co In this problem, we delve into the concepts of vector projection and orthogonality within the framework of three dimensional vectors. Inverse trigonometric functions and basic trigonometric equations1h 41m. © 1996– 2025 pearson all rights reserved. The magnitude of vector v is calculated using the square root of the sum of the squares of its components. practice problems are helpful in understanding and applying these concepts in different scenarios. This calculus 3 video tutorial explains how to find the vector projection of u onto v using the dot product and how to find the vector component of u orthogonal to v. That's an orthogonal projection onto the $x,z$ plane. if you are supposed to use some other projection (not orthogonal), however, there will be a different formula depending on the projection. This calculus 3 video tutorial explains how to find the vector projection of u onto v using the dot product and how to find the vector component of u orthogo.
Scalar And Vector Projections And Orthogonal Vectors 3 Example 1 The magnitude of vector v is calculated using the square root of the sum of the squares of its components. practice problems are helpful in understanding and applying these concepts in different scenarios. This calculus 3 video tutorial explains how to find the vector projection of u onto v using the dot product and how to find the vector component of u orthogonal to v. That's an orthogonal projection onto the $x,z$ plane. if you are supposed to use some other projection (not orthogonal), however, there will be a different formula depending on the projection. This calculus 3 video tutorial explains how to find the vector projection of u onto v using the dot product and how to find the vector component of u orthogo.
Comments are closed.