
Exploring Irrational Numbers And Number Sets 3 Pdf If you love our content, please feel free to try out our super affordable premium content. get access to all videos on the website(master learner pack):one m. Study the basics & operations on irrational numbers in a fun way. register with don't memorise and get access to all video lessons for a year.

Irrational Numbers Learn what irrational numbers are, how to identify them, and see clear examples like √2 and π. so irrational numbers are simply numbers that don’t come from dividing one whole number by another. that irrational numbers exist and are a natural part of the real number system. faqs about irrational numbers. Understand the concepts of number systems, operations & laws of real numbers, etc. enrol in class 9 math videos course & get access to 35 videos for a year. An irrational number is a number whose decimal representation is non terminating and non recurring. it cannot be expressed as a fraction of two integers. q: are all square roots irrational?. Unlock the mystery of irrational numbers in this easy to understand video, specially designed for icse class 9 students! 🎓in this lesson from chapter 1: num.
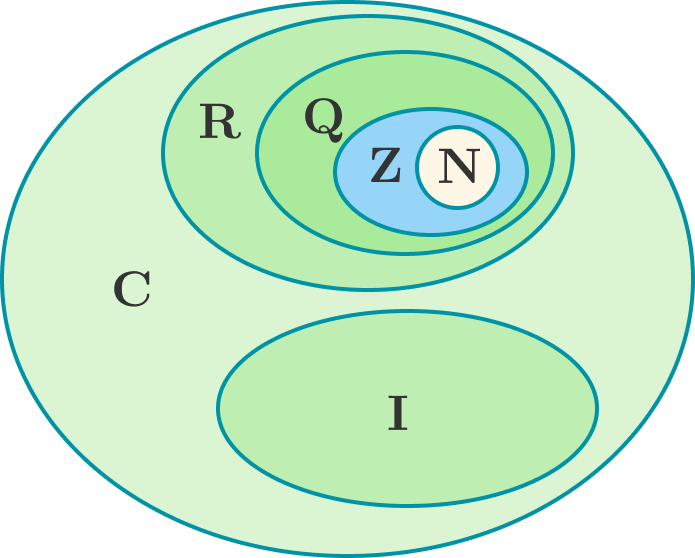
Irrational Numbers Brilliant Math Science Wiki An irrational number is a number whose decimal representation is non terminating and non recurring. it cannot be expressed as a fraction of two integers. q: are all square roots irrational?. Unlock the mystery of irrational numbers in this easy to understand video, specially designed for icse class 9 students! 🎓in this lesson from chapter 1: num. Irrational numbers: irrational numbers are those which can’t be expressed in fractional form, i.e., in p q p q form. they neither terminate nor do they repeat. they are also known as non terminating non repeating numbers. Irrational numbers are numbers that can not be expressed as the ratio of two integers. they are a subset of real numbers and can be expressed on the number line. and, the decimal expansion of an irrational number is neither terminating nor repeating. the symbol of irrational numbers is q’. Irrational numbers are real numbers that cannot be expressed as a simple fraction or ratio of two integers. in other words, they cannot be written in the form a b where a and b are integers and b ≠ 0. the decimal representation of an irrational number is non terminating and non repeating. Put simply, an irrational number is any real number (a positive or negative number, or 0) that can’t be written as a fraction. the fancier definition states that an irrational number can’t be expressed as a ratio of two integers – where p q and q≠0.

Irrational Numbers Chart Irrational numbers: irrational numbers are those which can’t be expressed in fractional form, i.e., in p q p q form. they neither terminate nor do they repeat. they are also known as non terminating non repeating numbers. Irrational numbers are numbers that can not be expressed as the ratio of two integers. they are a subset of real numbers and can be expressed on the number line. and, the decimal expansion of an irrational number is neither terminating nor repeating. the symbol of irrational numbers is q’. Irrational numbers are real numbers that cannot be expressed as a simple fraction or ratio of two integers. in other words, they cannot be written in the form a b where a and b are integers and b ≠ 0. the decimal representation of an irrational number is non terminating and non repeating. Put simply, an irrational number is any real number (a positive or negative number, or 0) that can’t be written as a fraction. the fancier definition states that an irrational number can’t be expressed as a ratio of two integers – where p q and q≠0.
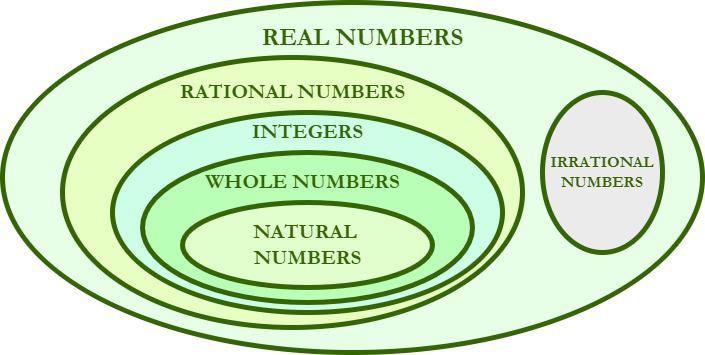
Irrational Numbers Definition Properties Examples Faqs Irrational numbers are real numbers that cannot be expressed as a simple fraction or ratio of two integers. in other words, they cannot be written in the form a b where a and b are integers and b ≠ 0. the decimal representation of an irrational number is non terminating and non repeating. Put simply, an irrational number is any real number (a positive or negative number, or 0) that can’t be written as a fraction. the fancier definition states that an irrational number can’t be expressed as a ratio of two integers – where p q and q≠0.

Irrational Numbers
