Why Do We Use The Fourier Transform
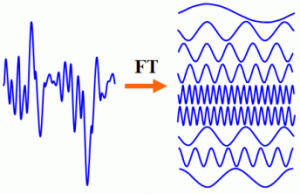
Why Do We Use Fourier Transform First and foremost, a fourier transform of a signal tells you what frequencies are present in your signal and in what proportions. example: have you ever noticed that each of your phone's number buttons sounds different when you press during a call and that it sounds the same for every phone model?. In particular, the scaling property of the fourier transform may be seen as saying: if we squeeze a function in x, its fourier transform stretches out in ξ. it is not possible to arbitrarily concentrate both a function and its fourier transform.
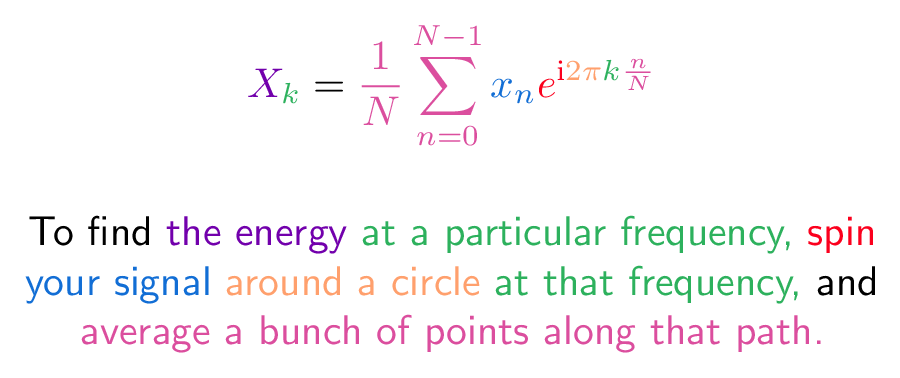
Fourier Transform Betterexplained This fact is the central philosophy behind fourier transforms (fourier was very french, so his name is pronounced a little wonky: “4 e yay”). a complicated signal can be broken down into simple waves. this break down, and how much of each wave is needed, is the fourier transform. Named after french mathematician joseph fourier, the fourier transform is a mathematical procedure that allows us to determine the frequency content of a function. for electrical engineers, the fourier transform is typically applied to functions of time that we call signals. At a high level, the fourier transform will allow us to convert our data to a different form where we can easily pick and choose the most important components and remove all of the noise. Whether in signal processing, image analysis, or solving differential equations, the fourier transform enables precise and efficient analysis, making it indispensable in both theoretical research and practical applications.

Solved What Is The Fourier Transform For Each Function Use Chegg At a high level, the fourier transform will allow us to convert our data to a different form where we can easily pick and choose the most important components and remove all of the noise. Whether in signal processing, image analysis, or solving differential equations, the fourier transform enables precise and efficient analysis, making it indispensable in both theoretical research and practical applications. The fourier transform is a powerful and essential tool in signal processing. it allows engineers to analyze, filter, and understand signals by converting them from the time domain into the frequency domain. Understand the fast fourier transform, a powerful algorithm essential for analyzing signal frequencies and enabling countless modern applications across science and engineering. In the world of signal processing and electrical engineering, the fourier transform stands as a powerful mathematical tool. it allows us to convert a time domain signal into its frequency domain representation, making it easier to analyse, manipulate, and understand. Here is just one example of its many applications. for a comprehensive and visually intuitive exploration of the fourier transform and its workings, i invite you to explore my book series on.

Fourier Transform Simple English Wikipedia The Free Encyclopedia The fourier transform is a powerful and essential tool in signal processing. it allows engineers to analyze, filter, and understand signals by converting them from the time domain into the frequency domain. Understand the fast fourier transform, a powerful algorithm essential for analyzing signal frequencies and enabling countless modern applications across science and engineering. In the world of signal processing and electrical engineering, the fourier transform stands as a powerful mathematical tool. it allows us to convert a time domain signal into its frequency domain representation, making it easier to analyse, manipulate, and understand. Here is just one example of its many applications. for a comprehensive and visually intuitive exploration of the fourier transform and its workings, i invite you to explore my book series on.
Comments are closed.